Ideał – w algebrze abstrakcyjnej podzbiór pierścienia o pewnych szczególnych własnościach. Pojęcie ideału zostało wprowadzone przez Dedekinda , jako uogólnienie pojęcia liczb idealnych rozważanych przez Kummera . Badania Dedekinda były kontynuowane przez Hilberta i szczególnie przez Emmę Noether .

Pojęcie ideału powstało przez wyodrębnienie pewnych własności, które posiadają pewne podzbiory zbioru liczb całkowitych takie jak zbiór liczb parzystych, czy ogólnie liczb podzielnych przez pewną liczbę k. Stąd też pochodzą pojęcia takie jak ideał pierwszy, który w pewien sposób uogólnia własności zbioru liczb podzielnych przez ustaloną liczbę pierwszą.

Ideały odgrywają w teorii pierścieni rolę analogiczną do podgrup normalnych w teorii grup . Pozwalają bowiem zdefiniować pierścień ilorazowy .

Definicja

Ideałem pierścienia przemiennego R nazywa się każdy podzbiór 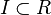taki, że:

1. jest podgrupą grupy addytywnej pierścienia
2. jeśli oraz , to

Zamiast pierwszego warunku wystarczy przyjąć, że zbiór I jest niepusty oraz, że spełniony jest warunek następujący:

jeśli 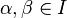, to

Niekiedy nie zakłada się przemienności pierścienia R. Wtedy powyższe warunki definiują ideał lewostronny pierścienia, natomiast jeśli zastąpimy drugi warunek następującym:

jeśli oraz , to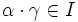

to otrzymamy definicję ideału prawostronnego.

Jeżeli A jest dowolnym podzbiorem pierścienia R, to przez 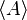oznaczamy najmniejszy (w sensie zawierania się zbiorów) ideał pierścienia R zawierający zbiór A. Można udowodnić, że

Ideał ten nazywamy ideałem generowanym przez zbiór A, a sam zbiór A zbiorem generatorów ideału .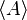

Typy ideałów

Z definicji natychmiast wynika, że sam pierścień R jest ideałem – ideały, które są właściwymi podzbiorami pierścienia R, nazywamy właściwymi. Ideał I jest właściwy wtedy i tylko wtedy, gdy nie zawiera 1.

Ideałem maksymalnym nazywamy ideał właściwy I o następującej własności: nie istnieje ideał właściwy 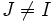taki, że . Korzystając z lematu Kuratowskiego-Zorna można udowodnić, że każdy ideał jest zawarty w pewnym ideale maksymalnym. Ponadto, ideał 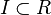jest maksymalny wtedy i tylko wtedy, gdy pierścień ilorazowy R / I jest ciałem .

Ideałem pierwszym nazywamy ideał o własności:

jeżeli , to lub .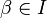

Każdy ideał maksymalny jest pierwszy. Ponadto, ideał 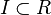jest pierwszy wtedy i tylko wtedy, gdy pierścień ilorazowy R / I nie posiada nietrywialnych dzielników zera (jest dziedziną całkowitości).

Jeżeli każdy ideał pierścienia jest pierwszy, to pierścień nazywamy pierścieniem ideałów pierwszych.

Ideałem głównym nazywamy ideał, który jest generowany przez jeden element. Jeżeli a jest takim elementem, to generowany przez a ideał główny jest zbiorem wszystkich elementów postaci dla .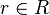

Jeżeli dla danego ideału I istnieje skończony zbiór A taki, że 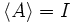, to ideał I nazywamy ideałem skończenie generowanym. Każdy ideał główny jest skończenie generowany.

Przykłady

• W dowolnym pierścieniu zbiór {0} jest ideałem, zwanym trywialnym.
• Zbiór wszystkich elementów pierścienia R jest ideałem w tym pierścieniu (zwanym niewłaściwym).
• W pierścieniu liczb całkowitych przykładem ideału jest zbiór wszystkich liczb parzystych. Ideałem jest również zbiór wszystkich liczb podzielnych przez 9. Ogólniej, każdy ideał pierścienia jest zbiorem wszystkich liczb podzielnych przez pewną liczbę naturalną k. Zatem jest pierścieniem ideałów głównych. Ideał pierścienia jest pierwszy, wtedy i tylko wtedy, gdy jest zbiorem liczb podzielnych przez pewną liczbę pierwszą.
• Jedynymi ideałami dowolnego ciała są ideał trywialny (złożony z samego zera) i niewłaściwy (całe ciało).
• Jeśli 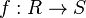jest homomorfizmem pierścieni, to jego jądro jest ideałem w pierścieniu R.
• Zbiór elementów nieodwracalnych pierścienia R tworzy ideał wtedy i tylko wtedy, gdy R zawiera dokładnie jeden ideał maksymalny.

Operacje na ideałach

Suma algebraiczna ideałów I i J pierścienia R, czyli zbiór

jest również ideałem w pierścieniu R.

Zbiór wszystkich iloczynów elementów dwu ideałów I i J nie musi być ideałem. Dlatego przez IJ rozumie się ideał generowany przez te iloczyny. Zatem:

Część wspólna ideałów również jest ideałem, podczas gdy teoriomnogościowa suma ideałów nie musi być ideałem, ale zawsze jest podzbiorem ideału IJ.

Część wspólna wszystkich ideałów pierwszych zawierających ideał I w pierścieniu R nazywana jest radykałem ideału I w pierścieniu R.

Zobacz też

• pierścień ,
• ideał maksymalny .