3 · 4 = 12, czyli dwanaście kropek można uporządkować w trzech rzędach po cztery (lub w czterech kolumnach po trzy).

Mnożenie – działanie dwuargumentowe będące jednym z czterech podstawowych działań arytmetycznych . Mnożone elementy to czynniki (określane również jako mnożna i mnożnik), a jego wynik to iloczyn. Może być ono traktowane jako zapis wielokrotnego dodawania elementu do siebie.

Na przykład:

gdzie liczby 3 i 4 są czynnikami, a 12 to ich iloczyn. Powyższe oznacza, że trzy grupy po cztery elementy to razem dwanaście elementów. Z każdej z powyższych równolicznych grup można wybrać kolejno po jednym elemencie i w ten sposób stworzyć cztery nowe grupy zawierające po trzy elementy:

.

W ten sposób , co w przypadku ogólnym nazywa się formalnie przemiennością . Należy mieć jednak na uwadze, że istnieją działania nazywane mnożeniami, które nie mają tej własności (zob. dalej).

Mnożenia liczb naturalnych o czynnikach będących liczbami ze zbioru

0,1,2,3,4,5,6,7,8,9,10 ( cyfry dziesiętnego systemu liczbowego uzupełnione o liczbę 10)

uczy się w pierwszych klasach szkoły podstawowej pod postacią tzw. tabliczki mnożenia . Dowolna liczba pomnożona przez zero daje w wyniku zero, podobnie dowolna liczba pomnożona przez jeden daje w wyniku tę liczbę (tzn. jedynka jest elementem neutralnym mnożenia).

Mnożenie pisemne liczb

Przykład

Algorytm pisemnego mnożenia najłatwiej wytłumaczyć na przykładzie. Obliczymy iloczyn liczb i . Należy zapisać jedną z liczb pod drugą tak, by cyfry oznaczające odpowiednio jedności, dziesiątki, setki itp. znajdowały się w jednej kolumnie (mniej precyzyjnie: wyrównać cyfry obu liczb do prawej):

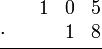
Następnie mnoży się poszczególne cyfry i zapisuje jedna pod drugą na odpowiedniej pozycji: jeżeli przyjąć, że pozycje cyfr numerowane są od prawej począwszy od zera, to cyfra dziesiątek i cyfra jednostek iloczynu dwóch cyfr powinny być zapisywane na pozycji będącej sumą pozycji mnożonych cyfr i o jeden mniejszej (jeżeli cyfra dziesiątek jest zerem, to zwykle się jej nie pisze). W ten sposób (mnożąc kolejno od prawej cyfry drugiej liczby przez kolejne cyfry pierwszej liczby):

Suma tak zapisanych iloczynów cyfr (przyjmując, że puste miejsca oznaczają zera) daje wynik:

Mnożenie liczb całkowitych przebiega podobnie, z tym iż mnoży się wartości bezwzględne , tzn. liczby bez znaku, i uzupełnia znak iloczynu minusem, jeżeli dokładnie jedna z nich była ujemna.

Jeżeli jeden (lub oba) z czynników jest pewną wielokrotnością liczby 10, tzn. na jej końcu znajduje się pewna liczba zer, to zamiast

oblicza się iloczyn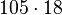

mnożąc przy tym tylko wspomniane czynniki, tzn. bez końcowych zer, mnożąc końcowy wynik przez iloczyn potęg, tzn. dopisując odpowiednią liczbę zer na jego końcu.

Podobnie ma się rzecz z ułamkami w zapisie dziesiętnym , gdyż są one ujemnymi potęgami liczby 10. Należy więc wykonać mnożenie tak, jakby w ich zapisie nie było przecinka, czyli znów zamiast 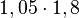należy obliczyć iloczyn 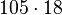po czym umieścić przecinek tak, by znajdował się na pozycji będącej sumą pozycji przecinków w czynnikach (licząc od prawej).

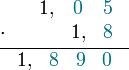
Uwaga: Mnożyć sposobem pisemnym można tylko w systemach pozycyjnych .

Algorytm

Sam algorytm mnożenia pisemnego polega na zapisaniu liczby naturalnej w postaci sumy kolejnych potęg dziesiątki. Niech i

,

.

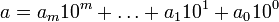Wówczas

przy czym trzecia równość odpowiada mnożeniu poszczególnych cyfr, a ostatnia – końcowemu sumowaniu.

Definicja

W dobrze znanych zbiorach liczbowych mnożenie definiowane jest osobno w każdym z nich za pomocą działania zdefiniowanego w prostszej strukturze:

• iloczyn dwóch liczb naturalnych a,b definiuje się jako -krotna sumę :

  .

można zapisać to rekurencyjnie: ;

• iloczyn dwóch liczb całkowitych i , gdzie określony jest wzorem

  ;

• iloczyn dwóch liczb wymiernych i , gdzie , a określony jest wzorem

  ;

• iloczyn dwóch liczb rzeczywistych i określa się następująco: jeżeli jest ciągiem Cauchy'ego zbieżnym do , a jest zbieżnym do , to ciąg jest ciągiem liczb wymiernych zbieżnym do ;
• iloczyn dwóch liczb zespolonych określony jest wzorem

.

Oznaczenia

Mnożenie oznacza się na ogół symbolem kropki, np. , czasami w miejsce kropki używa się znaku obróconego krzyżyka: , zaś w informatyce, z racji łatwej dostępności na klawiaturze komputera , przyjęło się używanie asterysku : a = b * c.

Jeśli nie prowadzi to do nieporozumień, symbol mnożenia w zapisie matematycznym często pomija się, np. zamiast pisze się .

Własności

Czynnik 1	Czynnik 2	Iloczyn
parzysty	całkowity	parzysty
całkowity	parzysty	parzysty
naturalny	naturalny	naturalny
całkowity	całkowity	całkowity
całkowity	wymierny	wymierny
wymierny	niewymierny	niewymierny lub zerowy
algebraiczny	algebraiczny	algebraiczny
algebraiczny	przestępny	przestępny lub zerowy
rzeczywisty	rzeczywisty	rzeczywisty
zespolony	zespolony	zespolony

Iloczyn skończonej liczby czynników

Niech A będzie zbiorem, w którym określono działanie łączne i mające element neutralny 1 (tzn. struktura jest monoidem ). Może to być np. zbiór liczb rzeczywistych (lub zespolonych) z mnożeniem. Wówczas definiujemy iloczyn indukcyjnie wzorami

i w podobny sposób definiujemy .

Notację tę można uogólnić, gdy dany jest dowolny warunek logiczny dotyczący wskaźnika, np.:

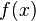• jest iloczynem czynników postaci dla każdego całkowitego x z przedziału [0,100),
• jest iloczynem czynników postaci 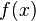dla każdego (niekoniecznie całkowitego).

Algebra

Mnożenie liczb zostało uogólnione na struktury algebraiczne nazwane pierścieniami (np. liczby całkowite) i ciałami (liczby wymierne, rzeczywiste, zespolone).

Rozpatruje się także mnożenie elementów ciała i przestrzeni liniowej nad tym ciałem, tzw. mnożenie przez skalar . Mnożeniem nazywa się często działanie w grupach w zapisie multiplikatywnym .

W tych strukturach mnożenie zwykle jest łączne i rozdzielne względem dodawania. Nie zawsze jest jednak przemienne , np. mnożenie macierzy i iloczyn wektorowy . Iloczyn wektorowy nie jest również łączny ; mnożenie nie jest łączne także w kwaternionach i oktonionach . Wynik mnożenia, nazywanego iloczynem skalarnym , pochodzi z innego zbioru niż czynniki.

Działanie mnożenia może mieć element neutralny , najogólniejszymi strukturami, w których działanie dwuargumentowe ma element neutralny są monoid (w którym działanie musi być łączne) i quasi-grupa (w którym działanie nie musi być łączne). Zwykle oznacza się go symbolem (inne rozpowszechnione oznaczenia: , , przy czym litery mogą być tak duże jak i małe) i nazywa jedynką (zob. pierścień z jedynką ).

Z istnieniem jedynki związany jest tzw. element odwrotny . Jeżeli iloczyn dwóch elementów jest jedynką, to elementy te nazywa się wzajemnie odwrotnymi. Najogólniejszą strukturą o tej własności jest pętla, czyli quasi-grupa z jedynką. Sama quasi-grupa to przykład struktury, w której można rozważać elementy odwrotne bez jedynki.

Zobacz też

• twierdzenie o mnożeniu ,
• potęgowanie ,
• silnia .