Liczby zespolone –
liczby
będące elementami
rozszerzenia ciała
liczb rzeczywistych
o
jednostkę urojoną
i, tj. pierwiastek
wielomianu
x2 + 1 (innymi słowy, jednostka urojona spełnia równanie i2 = − 1). Każda liczba zespolona z może być zapisana w postaci z = a + bi, gdzie a,b są pewnymi liczbami rzeczywistymi, nazywanymi odpowiednio częścią rzeczywistą oraz częścią urojoną liczby z.
Postać algebraiczna (kanoniczna)
Każdą liczbę zespoloną z można zapisać w postaci
- z = a + bi,
gdzie a i b są pewnymi liczbami rzeczywistymi oraz i jest tzw.
jednostką urojoną
, tj. i jest jednym z dwóch elementów zbioru liczb zespolonych, spełniającycm warunek i2 = − 1 (drugim elementem jest − i). Spotyka się czasami zapis "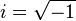 ", który nie jest formalnie poprawny ze względu na fakt, że również ( − i)2 = − 1, jest on jednak uznawany za pewien skrót myślowy i powszechnie akceptowany.
", który nie jest formalnie poprawny ze względu na fakt, że również ( − i)2 = − 1, jest on jednak uznawany za pewien skrót myślowy i powszechnie akceptowany.
Postać z = a + bi nazywana jest postacią algebraiczną (albo kanoniczną) liczby zespolonej z.
Dla liczby z = a + bi definiuje się jej
- część rzeczywistą jako
 (inne oznaczenia:
(inne oznaczenia:  ,
, - część urojoną jako
 (inne oznaczenia:
(inne oznaczenia: 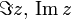 ).
).
Przykładowo liczba 7 − 5i jest liczbą zespoloną, której część rzeczywista wynosi 7, a część urojona − 5. Liczby rzeczywiste są utożsamiane z liczbami zespolonymi o części urojonej równej 0.
Liczby postaci z = 0 + bi nazywa się
liczbami urojonymi
.
Zapis alternatywny
W zastosowaniach
fizycznych
,
elektrycznych
,
elektrotechnicznych
itp. zapis  może okazać się mylący z powodu wykorzystywania w tych dziedzinach litery
może okazać się mylący z powodu wykorzystywania w tych dziedzinach litery  do innych celów, np. chwilowego
natężenia prądu elektrycznego
. Dlatego też stosuje się zapis niepowodujący podobnych kłopotów, mianowicie z = a + jb, w którym to j oznacza jednostkę urojoną.
do innych celów, np. chwilowego
natężenia prądu elektrycznego
. Dlatego też stosuje się zapis niepowodujący podobnych kłopotów, mianowicie z = a + jb, w którym to j oznacza jednostkę urojoną.
Wykres funkcji

wykonany za pomocą techniki kolorowania dziedziny. Odcień oznacza argument funkcji, zaś nasycenie reprezentuje jej moduł.
Równość
Dwie liczby zespolone są równe wtedy i tylko wtedy, gdy ich części rzeczywiste i urojone są sobie równe. Innymi słowy, liczby zespolone postaci  oraz
oraz  są sobie równe wtedy i tylko wtedy, gdy
są sobie równe wtedy i tylko wtedy, gdy  oraz
oraz  .
.
Działania
Dodawanie
,
odejmowanie
i
mnożenie
liczb zespolonych w postaci algebraicznej wykonuje się tak samo jak odpowiednie operacje na
wyrażeniach algebraicznych
, przy czym 

 .
.
Aby
podzielić
przez siebie dwie liczby zespolone, wystarczy pomnożyć dzielną i dzielnik przez liczbę sprzężoną do dzielnika (analogicznie do usuwania niewymierności z mianownika w wyrażeniach algebraicznych):

Płaszczyzna zespolona
Liczbom zespolonym można przyporządkować
wzajemnie jednoznacznie
wektory
na
płaszczyźnie
(zob. sekcję formalna konstrukcja), podobnie jak utożsamia się wektory na
prostej
z
liczbami rzeczywistymi
(w obu przypadkach można utożsamiać również same
punkty
, gdyż wspomniane wektory zaczepia się w początku
układów współrzędnych
).
Każdej więc liczbie zespolonej  można przyporządkować wektor
można przyporządkować wektor  i odwrotnie. Działania dodawania i mnożenia w liczbach zespolonych odpowiadają następującym działaniom na wektorach:
i odwrotnie. Działania dodawania i mnożenia w liczbach zespolonych odpowiadają następującym działaniom na wektorach:
 ,
,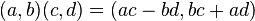 .
.
Tak określoną płaszczyznę określa się mianem płaszczyzny zespolonej. Interpretacja ta, dla której w specjalny sposób określono mnożenie, znana była już pod koniec
XVIII
wieku
Wesselowi
, mimo to przez długi czas jej autorstwo przypisywało się
Argandowi
, stąd też wspomnianą płaszczyzną nazywa się również płaszczyzną Arganda. Inną spotykaną nazwą jest też płaszczyzna Gaussa.
Moduł
Zauważmy, iż długość wektora 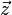 jest równa z
twierdzenia Pitagorasa
jest równa z
twierdzenia Pitagorasa
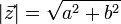 . Dla liczby z moduł definiujemy jako
. Dla liczby z moduł definiujemy jako  . Moduł liczby zespolonej ma analogiczne własności do
wartości bezwzględnej
liczby rzeczywistej spełniając przy tym definicję
normy
.
. Moduł liczby zespolonej ma analogiczne własności do
wartości bezwzględnej
liczby rzeczywistej spełniając przy tym definicję
normy
.
Argument
Niech  oznacza kąt, który wektor
oznacza kąt, który wektor 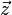 tworzy z prostą
tworzy z prostą  , oznaczmy go przez
, oznaczmy go przez  . Jest to tzw. argument. Widać, iż
. Jest to tzw. argument. Widać, iż  i
i 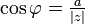 . Liczba zespolona różna od zera ma nieskończenie wiele argumentów, choć tylko jeden moduł.
. Liczba zespolona różna od zera ma nieskończenie wiele argumentów, choć tylko jeden moduł.
Argument liczby z spełniający nierówność  (czasami też równoważnie
(czasami też równoważnie  ) oznacza się przez
) oznacza się przez 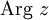 i nazywa argumentem głównym (wartością główną argumentu). W ten sposób
i nazywa argumentem głównym (wartością główną argumentu). W ten sposób  jest już
funkcją
na
jeden z powyższych zbiorów nieokreśloną jedynie dla
jest już
funkcją
na
jeden z powyższych zbiorów nieokreśloną jedynie dla  . Dla liczb rzeczywistych argument główny jest równy zeru dla liczb dodatnich oraz π dla ujemnych.
. Dla liczb rzeczywistych argument główny jest równy zeru dla liczb dodatnich oraz π dla ujemnych.
Postać trygonometryczna
Liczba zespolona może być zatem wyrażona przez długość jej wektora (moduł) oraz jego
kąt skierowany
(argument):
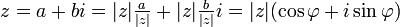 .
.
Powyższą postać liczby zespolonej nazywa się postacią trygonometryczną (z powodu użycia
funkcji trygonometrycznych
), biegunową (jest przedstawieniem liczby zespolonej we
współrzędnych biegunowych
) lub geometryczną (prowadzi do geometrycznej interpretacji liczb zespolonych na płaszczyźnie). Warto zauważyć, że postać algebraiczna odpowiada
współrzędnym prostokątnym
.
Liczby zespolone w postaci trygonometrycznej są równe, gdy ich moduły i argumenty są równe, tj.  oraz
oraz  są równe, gdy
są równe, gdy

oraz (istotne tylko dla  )
)
 .
.
Wzory pozwalające na przejście od postaci trygonometrycznej do algebraicznej są oczywiste:
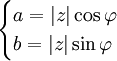 .
.
Przejście odwrotne jest nieco bardziej skomplikowane:
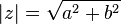 ,
,
 .
.
Powyższy wzór posiada dużo przypadków, jednakże w wielu
językach programowania
istnieje wariant funkcji
arcus tangens
, często nazywany arctan2 lub atan2, który przetwarza je wewnętrznie. Wzór korzystający z funkcji
arcus cosinus
wymaga mniejszej liczby przypadków:
 .
.
Mnożenie
Warto zwrócić uwagę na mnożenie liczb w postaci trygonometrycznej, niech

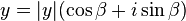
Wówczas iloczyn
 .
.
Stosując odpowiednie
tożsamości trygonometryczne
otrzymujemy ostatecznie
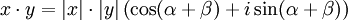 ,
,
co oznacza, że iloczyn dwóch liczb zespolonych posiada moduł będący iloczynem modułów mnożników oraz argument równy sumie argumentów mnożonych liczb.
Mnożenie przez  można zinterpretować jako
obrót
płaszczyzny o kąt
można zinterpretować jako
obrót
płaszczyzny o kąt  .
.
Wzór de Moivre'a
Potęgowanie za pomocą mnożenia liczb zespolonych w postaci algebraicznej prowadzi do obliczenia wartości wyrażenia  dla danego wykładnika
dla danego wykładnika  przy warunku
przy warunku  . Mimo że można korzystać z własności
trójkąta Pascala
, to porządkowanie tego wyrażenia może okazać się czasochłonne. Zwykle działanie to łatwiej przeprowadzić w postaci trygonometrycznej.
. Mimo że można korzystać z własności
trójkąta Pascala
, to porządkowanie tego wyrażenia może okazać się czasochłonne. Zwykle działanie to łatwiej przeprowadzić w postaci trygonometrycznej.
Rozpatrzmy  . Na podstawie reguły
indukcji matematycznej
zachodzi wzór
. Na podstawie reguły
indukcji matematycznej
zachodzi wzór
 .
.
Powyższy wzór jest również pomocny przy obliczaniu n-tej potęgi funkcji 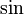 i
i  – należy wówczas obliczyć
– należy wówczas obliczyć  przy
przy  .
.
Pierwiastkowanie
Wzór de Moivre'a jest prawdziwy również dla
liczb wymiernych
. Każda liczba zespolona  posiada n różnych pierwiastków n-tego stopnia:
posiada n różnych pierwiastków n-tego stopnia:
![z_k = \sqrt[n]{|z|}\left(\cos \tfrac{\varphi + 2k\pi}{n} + i\sin \tfrac{\varphi + 2k\pi}{n}\right)](http://upload.wikimedia.org/math/4/1/8/418141e682d06ec27e38699e295a7892.png) , gdzie
, gdzie  oraz
oraz  .
.
Postać wykładnicza
Rozpatrzmy liczbę  wyrażając funkcje sin i cos za pomocą
funkcji wykładniczej
(zob.
wzory Eulera
):
wyrażając funkcje sin i cos za pomocą
funkcji wykładniczej
(zob.
wzory Eulera
):
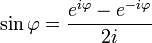

Mamy 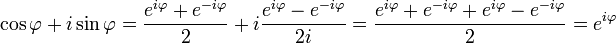 .
.
Zatem ostatecznie  .
.
Pierwiastki zespolone wyrażają się wówczas wzorem
![z_k = \sqrt[n]{|z|}\ e^{i\tfrac{\varphi + 2k\pi}{n}}](http://upload.wikimedia.org/math/3/5/4/354b60c91b9914dacc9b1fd26a0879ec.png) dla
dla  .
.
Sprzężenie
Niech  . Bardzo ważną operacją jest sprzężenie liczby zespolonej, jest ona najprostsza dla liczby w postaci algebraicznej:
. Bardzo ważną operacją jest sprzężenie liczby zespolonej, jest ona najprostsza dla liczby w postaci algebraicznej:

Działanie to powoduje odbicie wektora liczby zespolonej względem osi OX płaszczyzny zespolonej. Zatem liczba w postaci trygonometrycznej zachowa moduł, lecz jej argument ulegnie zmianie na  lub równoważnie – zmieni on znak na przeciwny. Skoro postać wykładnicza również zależy od modułu oraz argumentu, ta sama obserwacja dotyczy i jej. Prawdą jest też, że sprzężenie liczby rzeczywistej (liczby zespolonej o zerowej części urojonej) jest równe tej liczbie.
lub równoważnie – zmieni on znak na przeciwny. Skoro postać wykładnicza również zależy od modułu oraz argumentu, ta sama obserwacja dotyczy i jej. Prawdą jest też, że sprzężenie liczby rzeczywistej (liczby zespolonej o zerowej części urojonej) jest równe tej liczbie.
Sprzężenie przeprowadza
izomorficznie
ciało liczb zespolonych na siebie, jest zatem
automorfizmem
. Oprócz tożsamości jest to jedyny
ciągły
automorfizm tego ciała,
moc zbioru
nieciągłych automorfizmów wynosi zaś  . Działanie sprzężenia zespolonego jest
inwolucją
:
. Działanie sprzężenia zespolonego jest
inwolucją
:  .
.
Relacja porządku
Choć można sztucznie wprowadzić jakiś
porządek
liczb zespolonych (np.
porządek leksykograficzny
), to jednak taka
relacja
nie została określona i szerzej przyjęta. Nie da się bowiem sformułować jej w taki sposób, aby w zbiorze liczb zespolonych spełniała aksjomaty
ciała uporządkowanego
, jak w przypadku liczb rzeczywistych. Tak więc nie da się określić, która z dwóch liczb jest większa lub mniejsza. Można natomiast porównywać ich moduły oraz argumenty (główne), gdyż zarówno moduł jak i argument liczby zespolonej są liczbami rzeczywistymi.
Przykłady
Przedstawmy liczbę  (zob. sekcję dot. konstrukcji) w postaciach: algebraicznej, trygonometrycznej (biegunowej) i wykładniczej obliczając za każdym razem jej sprzężenie.
(zob. sekcję dot. konstrukcji) w postaciach: algebraicznej, trygonometrycznej (biegunowej) i wykładniczej obliczając za każdym razem jej sprzężenie.
Postać algebraiczna:
 ,
, .
.
Obliczamy
 ,
,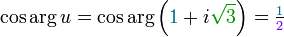 ,
, ,
, ,
,
podobnie
 .
.
Stąd postać trygonometryczna  oraz
oraz  to
to
 ,
, ,
,
zaś wykładnicza:
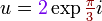 ,
, .
.
Konstrukcje i własności
Konstrukcja Hamiltona
Następująca formalna definicja liczb zespolonych pochodzi od
Hamiltona
,
matematyka
irlandzkiego
.
W
iloczynie kartezjańskim
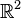 wprowadza się
działania
dodawania i mnożenia:
wprowadza się
działania
dodawania i mnożenia:
 ,
, ,
,
gdzie  .
.
Tak określona struktura  jest
ciałem
zwanym ciałem liczb zespolonych oznaczanym symbolem
jest
ciałem
zwanym ciałem liczb zespolonych oznaczanym symbolem  (od
ang.
complex – złożony)[1]. Wówczas
(od
ang.
complex – złożony)[1]. Wówczas  odpowiada wektorowi
odpowiada wektorowi 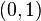 .
.
Ciało
Ciało
to struktura algebraiczna z działaniami dodawania, odejmowania, mnożenia i dzielenia, która spełnia określone prawa algebraiczne. Liczby zespolone jako ciało w szczególności mają więc:
-
element neutralny
dodawania („zero”),
 ,
, - element neutralny mnożenia („jedynka”),
 ,
, -
element odwrotny
dodawania (element przeciwny) dla każdej liczby zespolonej, dla liczby
 jest nim
jest nim  ,
, - element odwrotny mnożenia (odwrotność) dla dowolnej niezerowej liczby zespolonej, dla liczby
 jest nim
jest nim  .
.
Innymi ciałami są
liczby rzeczywiste
i
liczby wymierne
. Utożsamienie każdej liczby rzeczywistej 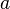 z liczbą zespoloną
z liczbą zespoloną  sprawia, że liczby rzeczywiste
sprawia, że liczby rzeczywiste  stają się podciałem
stają się podciałem  .
.
Liczby zespolone  mogą być scharakteryzowane również jako domknięcie topologiczne
liczb algebraicznych
oraz jako domknięcie algebraiczne
mogą być scharakteryzowane również jako domknięcie topologiczne
liczb algebraicznych
oraz jako domknięcie algebraiczne  , co opisano dalej.
, co opisano dalej.
Reprezentacja macierzowa
Chociaż niezbyt użyteczne, alternatywne reprezentacje ciała liczb zespolonych mogą dać pewien wgląd w jego naturę. Jedna ze szczególnie eleganckich reprezentacji przedstawia każdą liczbę zespoloną jako 2×2-
macierz
o współczynnikach
rzeczywistych
, które rozciągają i obracają punkty (wektory) płaszczyzny. Każda taka macierz jest postaci
 ,
,
gdzie  . Suma i iloczyn dwóch takich macierzy także ma tę postać, a działanie mnożenia macierzy tego typu jest
przemienne
. Każda niezerowa macierz tego typu jest odwracalna, a jej odwrotność także ma tę postać. Stąd macierze tego typu są
ciałem
izomorficznym
z ciałem liczb zespolonych. Każda taka macierz może być zapisana jako
. Suma i iloczyn dwóch takich macierzy także ma tę postać, a działanie mnożenia macierzy tego typu jest
przemienne
. Każda niezerowa macierz tego typu jest odwracalna, a jej odwrotność także ma tę postać. Stąd macierze tego typu są
ciałem
izomorficznym
z ciałem liczb zespolonych. Każda taka macierz może być zapisana jako
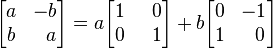 ,
,
co sugeruje, że liczba rzeczywista 1 powinna być utożsamiana z
macierzą identycznościową
 ,
,
a jednostka urojona i z
 ,
,
obrotem o  w kierunku przeciwnym do ruchu wskazówek zegara. Kwadrat drugiej z macierzy rzeczywiście jest równy 2×2-macierzy reprezentującej − 1.
w kierunku przeciwnym do ruchu wskazówek zegara. Kwadrat drugiej z macierzy rzeczywiście jest równy 2×2-macierzy reprezentującej − 1.
Kwadrat modułu liczby zespolonej wyrażonej jako macierz jest równy
wyznacznikowi
tej macierzy.
 .
.
Jeżeli macierz postrzegana jest jako przekształcenie płaszczyzny, to obraca ono punkty o kąt równy argumentowi liczby zespolonej i skaluje o wspólczynnik równy modułowi liczby zespolonej. Sprzężenie liczby zespolonej 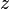 odpowiada przekształceniu, które obraca o ten sam kąt, co
odpowiada przekształceniu, które obraca o ten sam kąt, co 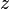 , lecz w przeciwnym kierunku i skaluje w ten sam sposób, co
, lecz w przeciwnym kierunku i skaluje w ten sam sposób, co 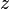 ; może to być oddane jako
transpozycja
macierzy odpowiadającej
; może to być oddane jako
transpozycja
macierzy odpowiadającej 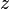 .
.
Jeżeli elementy macierzy same są liczbami zespolonymi, to powstała w ten sposób algebra może być utożsamiana z
kwaternionami
. Innymi słowy, ta reprezentacja macierzowa jest sposobem wyrażenia
konstrukcji Cayleya-Dicksona
algebr.
Istnieją dwa
wektory własne
2×2-macierzy reprezentującej liczbę zespoloną: rzeczona liczba zespolona i jej sprzężenie.
Rzeczywista przestrzeń liniowa
Ciało  jest dwuwymiarową rzeczywistą
przestrzenią liniową
. W przeciwieństwie jednak do liczb rzeczywistych, liczby zespolone nie mogą być w żaden sposób
uporządkowane liniowo
tak, by było to zgodne z działaniami arytmetycznymi w nich określonymi:
jest dwuwymiarową rzeczywistą
przestrzenią liniową
. W przeciwieństwie jednak do liczb rzeczywistych, liczby zespolone nie mogą być w żaden sposób
uporządkowane liniowo
tak, by było to zgodne z działaniami arytmetycznymi w nich określonymi:  nie może być przekształcone w
ciało uporządkowane
. Ogólniej: żadne ciało zawierające pierwiastek z
nie może być przekształcone w
ciało uporządkowane
. Ogólniej: żadne ciało zawierające pierwiastek z  nie może być uporządkowane.
nie może być uporządkowane.
W ogólności  -
liniowe
przekształcenia
-
liniowe
przekształcenia  są postaci
są postaci

gdzie 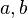 są współczynnikami zespolonymi. Tylko pierwszy wyraz jest
są współczynnikami zespolonymi. Tylko pierwszy wyraz jest  -liniowy i tylko on jest
holomorficzny
, drugi jest różniczkowalny w sensie rzeczywistym, lecz nie spełnia
równań Cauchy'ego-Riemanna
.
-liniowy i tylko on jest
holomorficzny
, drugi jest różniczkowalny w sensie rzeczywistym, lecz nie spełnia
równań Cauchy'ego-Riemanna
.
Funkcja
- f(z) = az,
odpowiada obrotom złożonym ze skalowaniem (która nie zmienia orientacji), zaś funkcja

odpowiada symetriom złożonym ze skalowaniem (zmienia orientację).
Rozwiązania równań wielomianowych
Pierwiastek
wielomianu
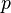 to liczba zespolona
to liczba zespolona 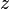 spełniająca
spełniająca  . Zaskakującym wynikiem
analizy zespolonej
jest to, iż wszystkie wielomiany stopnia
. Zaskakującym wynikiem
analizy zespolonej
jest to, iż wszystkie wielomiany stopnia  o współczynnikach rzeczywistych lub zespolonych mają dokładnie
o współczynnikach rzeczywistych lub zespolonych mają dokładnie  pierwiastków zespolonych (licząc pierwiastki wielokrotnie zgodnie z ich wielokrotnością). Wynik ten znany jest jako
podstawowe twierdzenie algebry
i pokazuje, że liczby zespolone są
ciałem algebraicznie domkniętym
. Rzeczywiście, są one
domknięciem algebraicznym
liczb rzeczywistych, jak opisano niżej.
pierwiastków zespolonych (licząc pierwiastki wielokrotnie zgodnie z ich wielokrotnością). Wynik ten znany jest jako
podstawowe twierdzenie algebry
i pokazuje, że liczby zespolone są
ciałem algebraicznie domkniętym
. Rzeczywiście, są one
domknięciem algebraicznym
liczb rzeczywistych, jak opisano niżej.
Konstrukcja algebraiczna
Jedna z możliwych konstrukcji ciała liczb zespolonych polega na
rozszerzeniu ciała
liczb rzeczywistych  o pierwiastek wielomianu x2 + 1. Aby skonstruować to rozszerzenie, należy wziąć pierścień
o pierwiastek wielomianu x2 + 1. Aby skonstruować to rozszerzenie, należy wziąć pierścień ![\mathbb R[x]](http://upload.wikimedia.org/math/e/a/9/ea9bb5df2d9684e02f2046d0aac09277.png) wielomianów o współczynnikach. Wielomian x2 + 1 jest
nierozkładalny
nad
wielomianów o współczynnikach. Wielomian x2 + 1 jest
nierozkładalny
nad  , skąd ideał przez niego generowany (x2 + 1) jest maksymalny, a więc
pierścień ilorazowy
, skąd ideał przez niego generowany (x2 + 1) jest maksymalny, a więc
pierścień ilorazowy
![\mathbb R[x]/(x^2 + 1)](http://upload.wikimedia.org/math/1/d/d/1ddeb6226017ad60607a5147586dc960.png) jest ciałem. Rozszerzenie to zawiera dwa pierwiastki kwadratowe z –1; wybiera się jeden z nich i oznacza symbolem
jest ciałem. Rozszerzenie to zawiera dwa pierwiastki kwadratowe z –1; wybiera się jeden z nich i oznacza symbolem  . Zbiór
. Zbiór  stanowi bazę tego rozszerzenia ciała liczb rzeczywistych. Dokładniej: każdy element tego rozszerzenia można zapisać w postaci
stanowi bazę tego rozszerzenia ciała liczb rzeczywistych. Dokładniej: każdy element tego rozszerzenia można zapisać w postaci

dla pewnych a,b rzeczywistych.
Algebraiczna domkniętość
Chociaż dodano wyłącznie pierwiastki  , to otrzymane ciało ciało liczb zespolonych jest
algebraicznie domknięte
– każdy wielomian o współczynnikach w
, to otrzymane ciało ciało liczb zespolonych jest
algebraicznie domknięte
– każdy wielomian o współczynnikach w  można rozłożyć na wielomiany liniowe o współczynnikach z
można rozłożyć na wielomiany liniowe o współczynnikach z  . Ponieważ każde ciało ma tylko jedno, co do izomorfizmu, domknięcie algebraiczne, liczby zespolone mogą być scharakteryzowane jako domknięcie algebraiczne liczb rzeczywistych.
. Ponieważ każde ciało ma tylko jedno, co do izomorfizmu, domknięcie algebraiczne, liczby zespolone mogą być scharakteryzowane jako domknięcie algebraiczne liczb rzeczywistych.
Charakteryzacja algebraiczna
Opisywane rozszerzenie odpowiada dobrze znanej płaszczyźnie zespolonej, lecz fakt ten charakteryzuje je wyłącznie algebraicznie. Ciało  jest
scharakteryzowane
co do izomorfizmu ciał przez następujące trzy własności:
jest
scharakteryzowane
co do izomorfizmu ciał przez następujące trzy własności:
Jedną z konsekwencji tej charakteryzacji jest to, że  zawiera wiele podciał właściwych izomorficznych z
zawiera wiele podciał właściwych izomorficznych z  (to samo jest prawdą dla
(to samo jest prawdą dla  , które zawiera wiele podciał izomorficznych do siebie). Jak opisano poniżej, aby odróżnić te podciała od samych ciał
, które zawiera wiele podciał izomorficznych do siebie). Jak opisano poniżej, aby odróżnić te podciała od samych ciał  i
i  wymagane są rozważania topologiczne.
wymagane są rozważania topologiczne.
Charakteryzacja topologiczna
Jak zauważono wyżej, algebraiczna charakteryzacja  nie dostarcza pewnych z jego najważniejszych własności topologicznych. Własności te są kluczowe podczas studiowania
analizy zespolonej
, gdzie liczby zespolone badane są jako
ciało topologiczne
.
nie dostarcza pewnych z jego najważniejszych własności topologicznych. Własności te są kluczowe podczas studiowania
analizy zespolonej
, gdzie liczby zespolone badane są jako
ciało topologiczne
.
Następujące własności charakteryzują  jako ciało topologiczne:[]
jako ciało topologiczne:[]
 jest ciałem,
jest ciałem, zawiera podzbiór
zawiera podzbiór  niezerowych elementów spełniających:
niezerowych elementów spełniających: jest zamknięte ze względu na dodawanie, mnożenie i branie elementów odwrotnych,
jest zamknięte ze względu na dodawanie, mnożenie i branie elementów odwrotnych,- jeżeli
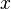 i
i 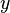 są różnymi elementami
są różnymi elementami  , to tak
, to tak 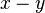 , jak i
, jak i  należą do
należą do  ,
, - jeżeli
 jest niepustym podzbiorem
jest niepustym podzbiorem  , to
, to  dla pewnego
dla pewnego  ,
,
 ma nietrywialny, będący
inwolucją
automorfizm
ma nietrywialny, będący
inwolucją
automorfizm
 , który dla ustalonego
, który dla ustalonego  spełnia własność, że
spełnia własność, że  należy do
należy do  dla dowolnego niezerowygo
dla dowolnego niezerowygo  .
.
Dla danego ciała o tych własnościach można zdefiniować topologię biorąc zbiory
jako
bazę
, gdzie x przebiega to ciało, a 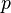 przebiega
przebiega  .
.
Aby przekonać się, że te własności charakteryzują  jako
ciało topologiczne
, należy zauważyć, że
jako
ciało topologiczne
, należy zauważyć, że 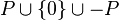 to ciało
uporządkowane zupełnie w sensie Dedekinda
, które może być w związku z tym utożsamiane z
liczbami rzeczywistymi
to ciało
uporządkowane zupełnie w sensie Dedekinda
, które może być w związku z tym utożsamiane z
liczbami rzeczywistymi
 poprzez jednoznacznie wyznaczony izomorfizm ciał. Z ostatniej własności łatwo wynika, że
grupa Galois
nad liczbami rzeczywistymi ma rząd równy dwa, co uzupełnia charakteryzację.
poprzez jednoznacznie wyznaczony izomorfizm ciał. Z ostatniej własności łatwo wynika, że
grupa Galois
nad liczbami rzeczywistymi ma rząd równy dwa, co uzupełnia charakteryzację.
Lew Pontriagin
pokazał, że jedynymi
spójnymi
lokalnie zwartymi
ciałami topologicznymi
są  oraz
oraz  . Fakt ten umożliwia jeszcze jedną charakteryzację
. Fakt ten umożliwia jeszcze jedną charakteryzację  jako ciała topologicznego, ponieważ
jako ciała topologicznego, ponieważ  może być odróżnione od
może być odróżnione od  poprzez uwagę, iż niezerowe liczby zespolone są
spójne
w przeciwieństwie do niezerowych liczb rzeczywistych.
poprzez uwagę, iż niezerowe liczby zespolone są
spójne
w przeciwieństwie do niezerowych liczb rzeczywistych.
Historia
Liczby zespolone zostały wprowadzone do
matematyki
przez
Girolama Cardana
. Nadał on w szczególności liczbie i nazwę
jednostki urojonej
, nie wierząc w rzeczywiste istnienie takiego obiektu, a jedynie uznając go za pomocniczy element w rachunku, mającym w zamierzeniu dać pierwiastki
równania wielomianowego trzeciego stopnia
(tzw. wzory Cardano).
Liczbami zespolonymi zajmowali się wielcy matematycy tacy jak
Hamilton
, czy
Euler
(zob.
wzór Eulera
). Jest to ciekawy przykład pojęcia o fundamentalnym znaczeniu dla techniki (m.in.
elektrotechniki
), które znalazło swoje główne zastosowanie po kilkuset latach od odkrycia. Formalne określenie zbioru liczb zespolonych jako zbioru 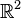 , z odpowiednio zdefiniowanymi działaniami dodawania i mnożenia, pochodzi od
Hamiltona
.
, z odpowiednio zdefiniowanymi działaniami dodawania i mnożenia, pochodzi od
Hamiltona
.
- Ta sekcja jest . Jeśli możesz, .
Zastosowania
Liczby zespolone są dość wygodnym sposobem zapisu punktów płaszczyzny. Analizą
euklidesowej przestrzeni
dwuwymiarowej zajmuje się w ogólności tzw. analiza wielowymiarowa, zaś analizą przestrzeni zespolonej
analiza zespolona
.
Liczby zespolone znajdują zastosowanie m.in. w:
Liczby zespolone można rozumieć m.in. jako szczególny przypadek
kwaternionów
,
oktaw Cayleya
,
sedenionów
.
Zobacz też
Przypisy
- ↑ istnieje też nieużywane powszechnie polskie oznaczenie szkolne:
Linki zewnętrzne