Algebra Boole'a –
struktura algebraiczna
stosowana w
matematyce
,
informatyce
teoretycznej oraz
elektronice cyfrowej
. Jej nazwa pochodzi od nazwiska
angielskiego
matematyka,
filozofa
i logika
George'a Boole'a
. Teoria algebr Boole'a jest działem matematyki na styku teorii
porządków częściowych
,
algebry
,
logiki matematycznej
i
topologii
.
Typowymi przykładami algebr Boole'a są:
rodzina
wszystkich
podzbiorów
ustalonego
zbioru
wraz działaniami na zbiorach jako operacjami algebry oraz dwuelementowa algebra
wartości logicznych
{0, 1} z działaniami
koniunkcji
,
alternatywy
i
negacji
.
Definicja
Algebra Boole'a to struktura algebraiczna  , w której
, w której  i
i  są
działaniami dwuargumentowymi
, ˜ jest operacją jednoargumentową, a 0 i 1 są wyróżnionymi różnymi elementami zbioru
są
działaniami dwuargumentowymi
, ˜ jest operacją jednoargumentową, a 0 i 1 są wyróżnionymi różnymi elementami zbioru 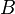 , spełniająca następujące warunki dla wszystkich
, spełniająca następujące warunki dla wszystkich  :
:
Oznaczenia
Różne oznaczenia| Suma | Iloczyn | Negacja |
|---|
 |  | ˜ |
| + |  |  |
| + |  | − |
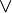 |  |  |
Istnieją co najmniej trzy różne, szeroko rozpowszechnione tradycje oznaczeń w teorii algebr Boole'a. W definicji sformułowanej powyżej użyto symboli  , ale w częstym użyciu są również
, ale w częstym użyciu są również  oraz
oraz  . Symbole oznaczające operacje dwuczłonowe algebry Boole'a są prawie zawsze wprowadzane przez wybór jednej z par
. Symbole oznaczające operacje dwuczłonowe algebry Boole'a są prawie zawsze wprowadzane przez wybór jednej z par  ,
,  albo
albo  . W oznaczeniach operacji jednoargumentowej algebry istnieje mniejsza konsekwencja i można się spotkać zarówno z symbolami
. W oznaczeniach operacji jednoargumentowej algebry istnieje mniejsza konsekwencja i można się spotkać zarówno z symbolami  jak i
jak i  .
.
System oznaczeń przedstawiony powyżej (i dalej przyjmowany w tym artykule) jest używany np. w podręczniku
Heleny Rasiowej
.
W badaniach
teorio-mnogościowych
aspektów algebr Boole'a przeważa tradycja używania oznaczeń  . Ten sam system został też wybrany za wiodący przez redaktorów
monografii
Handbook of Boolean Algebras.
. Ten sam system został też wybrany za wiodący przez redaktorów
monografii
Handbook of Boolean Algebras.
Z kolei symbole 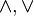 zgodne z oznaczeniami w teorii
krat
są częściej używane w kontekstach algebraicznych (i teorio-kratowych).
zgodne z oznaczeniami w teorii
krat
są częściej używane w kontekstach algebraicznych (i teorio-kratowych).
Spotykane są też inne kombinacje tychże symboli lub wręcz inne symbole (na przykład & w miejsce  , lub
, lub  zamiast
zamiast  ). W elektronice i informatyce często stosuje się OR, AND oraz NOT w miejsce
). W elektronice i informatyce często stosuje się OR, AND oraz NOT w miejsce  ,
,  oraz ˜.
oraz ˜.
Minimalna aksjomatyzacja
Powyższa (tradycyjna) definicja algebry Boole'a nie jest minimalna, np. nie jest konieczne wprowadzanie w niej symboli 0 i 1. Mogą one być konsekwencją aksjomatyki a nie niezbędną dla niej definicją. 0 można zastąpić przez 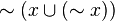 a 1 przez
a 1 przez  . Dzięki prawom de Morgana można też z aksjomatyki wyeliminować działanie
. Dzięki prawom de Morgana można też z aksjomatyki wyeliminować działanie  lub
lub  . (W istocie wszystkie działania można tak naprawdę zastąpić jednym –
dysjunkcją
(NAND) lub
binegacją
(NOR)).
. (W istocie wszystkie działania można tak naprawdę zastąpić jednym –
dysjunkcją
(NAND) lub
binegacją
(NOR)).
Istnieją równoważne, ale oszczędniejsze definicje algebry Boole'a. Przykładowy układ niezależnych
aksjomatów
to:
 jest przemienne,
jest przemienne, jest łączne,
jest łączne,- aksjomat Huntingtona:
 .
.
Inny taki układ to:
 jest przemienne
jest przemienne jest łączne
jest łączne- aksjomat Robbinsa:

Istnieją też systemy z jednym aksjomatem.
Przykłady
Najprostsza algebra Boole'a ma tylko dwa elementy, 0 i 1, a operacje tej algebry są zdefiniowane przez następujące tabele działań:
|  | 0 | 1 |
|---|
| 0 | 0 | 0 |
|---|
| 1 | 0 | 1 |
|---|
| | | | | | |
Algebra ta stanowi podstawę elektroniki cyfrowej.
Jeśli  jest
ciałem podzbiorów
zbioru X, to
jest
ciałem podzbiorów
zbioru X, to 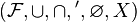 jest algebrą Boole'a (gdzie
jest algebrą Boole'a (gdzie  oznacza operację
dopełnienia
).
oznacza operację
dopełnienia
).
Niech 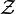 będzie zbiorem
zdań
w
rachunku zdań
. Niech
będzie zbiorem
zdań
w
rachunku zdań
. Niech  będzie relacją dwuargumentową na zbiorze
będzie relacją dwuargumentową na zbiorze 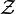 określoną jako:
określoną jako:
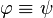 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy jest
tautologią
rachunku zdań.
jest
tautologią
rachunku zdań.
Można sprawdzić, że  jest
relacją równoważności
na zbiorze
jest
relacją równoważności
na zbiorze 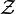 . Na zbiorze X wszystkich
klas abstrakcji
. Na zbiorze X wszystkich
klas abstrakcji
![[\varphi]](http://upload.wikimedia.org/math/7/8/d/78db87833111c04d5aa35e3a403b7363.png) relacji
relacji  można wprowadzić operacje
można wprowadzić operacje  przez następujące formuły:
przez następujące formuły:
![[\varphi] \cup [\psi] := [\varphi\vee\psi]](http://upload.wikimedia.org/math/b/8/d/b8da80848400be3a55ec91b80bf4b4bd.png) ,
,![[\varphi] \cap [\psi] := [\varphi\wedge\psi]](http://upload.wikimedia.org/math/d/d/b/ddb1d453789b26cd840e82b46a2787d8.png) ,
,![\sim[\varphi] := [\neg\varphi]](http://upload.wikimedia.org/math/d/5/7/d570eef470bea98b4001b9c3fa5065cc.png) .
.
W ten sposób otrzymuje się poprawnie zdefiniowane operacje na zbiorze X (tzn. wynik nie zależy od wyboru reprezentantów klas abstrakcji), a ![(X,\cup,\cap,\sim,[p\wedge\neg p],[p\vee\neg p])](http://upload.wikimedia.org/math/4/5/8/4586c22a21e5d8ec9a2ffc77a6be3496.png) jest algebrą Boole'a. Algebra ta jest nazywana algebrą Lindenbauma-Tarskiego.
jest algebrą Boole'a. Algebra ta jest nazywana algebrą Lindenbauma-Tarskiego.
Algebry Lindenbauma-Tarskiego rozważa się również dla
języków pierwszego rzędu
. Niech  będzie zbiorem
zdań
w ustalonym alfabecie τ i niech
będzie zbiorem
zdań
w ustalonym alfabecie τ i niech  będzie niesprzeczną teorią w tym samym języku. Relację dwuargumentową
będzie niesprzeczną teorią w tym samym języku. Relację dwuargumentową  na zbiorze
na zbiorze  można wprowadzić przez określenie
można wprowadzić przez określenie
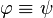 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy .
.
Wówczas  jest relacją równoważności na zbiorze
jest relacją równoważności na zbiorze  . Podobnie jak wcześniej:
. Podobnie jak wcześniej:
![[\varphi] \cup [\psi] := [\varphi\vee\psi]](http://upload.wikimedia.org/math/b/8/d/b8da80848400be3a55ec91b80bf4b4bd.png) ,
,![[\varphi] \cap [\psi] := [\varphi\wedge\psi]](http://upload.wikimedia.org/math/d/d/b/ddb1d453789b26cd840e82b46a2787d8.png) ,
,![\sim[\varphi] := [\neg\varphi]](http://upload.wikimedia.org/math/d/5/7/d570eef470bea98b4001b9c3fa5065cc.png) .
.
Można pokazać, że ![({\bold Z}/\equiv,\cup,\cap,\sim,[\psi\wedge\neg \psi]_\equiv,[\psi\vee\neg \psi]_\equiv)](http://upload.wikimedia.org/math/e/0/e/e0e446dabea91421b1fe50eea85a848e.png) jest algebrą Boole'a.
jest algebrą Boole'a.
Własności
Niech  będzie algebrą Boole'a. Dla wszystkich
będzie algebrą Boole'a. Dla wszystkich  zachodzi:
zachodzi:








prawa De Morgana
:


podwójne przeczenie
:

Uporządkowanie
W zbiorze 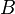 wprowadza się porządek boole'owski
wprowadza się porządek boole'owski  :
:
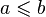 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 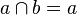
Tak zdefiniowana
relacja
 jest
częściowym porządkiem
na zbiorze
jest
częściowym porządkiem
na zbiorze  . Zbiór
. Zbiór  z relacją ≤ jest kratą rozdzielną.
z relacją ≤ jest kratą rozdzielną.
Ideały, algebry ilorazowe i homomorfizmy
Niepusty zbiór  jest
ideałem
w algebrze
jest
ideałem
w algebrze  , jeśli są spełnione następujące dwa warunki:
, jeśli są spełnione następujące dwa warunki:
 , oraz
, oraz .
.
Każdy ideał zawiera element  . Ideał, który nie zawiera elementu
. Ideał, który nie zawiera elementu  , nazywany jest ideałem właściwym. Jedynym niewłaściwym ideałem jest całe
, nazywany jest ideałem właściwym. Jedynym niewłaściwym ideałem jest całe  .
.
Pojęciem dualnym jest pojęcie
filtru
: niepusty zbiór 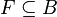 jest filtrem w algebrze
jest filtrem w algebrze  , jeśli:
, jeśli:

oraz
 .
.
Każdy filtr zawiera element  . Filtr, który nie zawiera elementu
. Filtr, który nie zawiera elementu  , nazywany jest filtrem właściwym. Jedynym niewłaściwym filtrem jest całe
, nazywany jest filtrem właściwym. Jedynym niewłaściwym filtrem jest całe 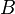 .
.
Niech  będzie właściwym ideałem w algebrze
będzie właściwym ideałem w algebrze  . Niech
. Niech  będzie relacją dwuczłonową na
będzie relacją dwuczłonową na 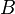 taką, że
taką, że
 wtedy i tylko wtedy gdy
wtedy i tylko wtedy gdy  .
.
Wówczas  jest relacją równoważności na
jest relacją równoważności na 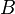 . W zbiorze
. W zbiorze  klas abstrakcji tej relacji można zdefiniować działania
klas abstrakcji tej relacji można zdefiniować działania  :
:
![[a] \vee [b] := [a\cup b]](http://upload.wikimedia.org/math/9/6/3/9630cdb27d36f00fa29aec9be2c9b64e.png) ,
,![[a] \wedge [b] := [a\cap b]](http://upload.wikimedia.org/math/9/9/2/992ef8d4c925ef89fe1ad80dd16dd4a1.png) ,
,![\neg [a] := [\sim a]](http://upload.wikimedia.org/math/e/9/a/e9a3493c14da4c2ad0286fa5e465075f.png) .
.
Pokazuje się, że powyższe definicje są poprawne (tzn. wynik operacji nie zależy od wyboru reprezentantów z klas abstrakcji) oraz że ![(B/_{\approx_I},\vee,\wedge,\neg,[0],[1])](http://upload.wikimedia.org/math/1/7/9/17908d5c5220bfb07c5c79e2144cb96d.png) jest algebrą Boole'a. Algebra ta jest nazywana algebrą ilorazową i jest oznaczana przez
jest algebrą Boole'a. Algebra ta jest nazywana algebrą ilorazową i jest oznaczana przez  .
.
Niech  będzie algebrą Boole'a i niech
będzie algebrą Boole'a i niech  będzie
funkcją
odwzorowującą
będzie
funkcją
odwzorowującą 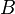 w
w  . Mówimy, że funkcja h jest
homomorfizmem
algebr Boole'a, jeśli zachowuje ona działania w algebrze, tzn. dla wszystkich
. Mówimy, że funkcja h jest
homomorfizmem
algebr Boole'a, jeśli zachowuje ona działania w algebrze, tzn. dla wszystkich  zachodzą trzy równości:
zachodzą trzy równości:
 ,
, ,
, .
.
Jeśli dodatkowo  jest
funkcją wzajemnie jednoznaczną
z
jest
funkcją wzajemnie jednoznaczną
z 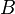 na
na  , to funkcja
, to funkcja  zwana jest
izomorfizmem
algebr Boole'a.
zwana jest
izomorfizmem
algebr Boole'a.
Jeśli  jest ideałem w algebrze
jest ideałem w algebrze  , to odwzorowanie
, to odwzorowanie ![a\mapsto [a]_{\approx_I}:{\mathbb B}\to {\mathbb B}/I](http://upload.wikimedia.org/math/7/e/5/7e57ff5d095c7730013a7025adb38ec8.png) jest homomorfizmem.
jest homomorfizmem.
Jeśli  jest algebrą Boole'a oraz
jest algebrą Boole'a oraz  jest homomorfizmem
na
jest homomorfizmem
na
 , to
, to  jest ideałem w algebrze
jest ideałem w algebrze  a algebra ilorazowa
a algebra ilorazowa  jest izomorficzna z
jest izomorficzna z  .
.
Autodualność
Niech  (operacje
(operacje  i
i  zostały zamienione rolami, podobnie jak stałe 0 i 1). Wtedy także
zostały zamienione rolami, podobnie jak stałe 0 i 1). Wtedy także  jest algebrą Boole'a izomorficzną z wyjściową algebrą
jest algebrą Boole'a izomorficzną z wyjściową algebrą  . Kanoniczny izomorfizm d tych dwóch algebr jest swoją własną odwrotnością (jest
inwolucją
zbioru B) i jest dany wzorem:
. Kanoniczny izomorfizm d tych dwóch algebr jest swoją własną odwrotnością (jest
inwolucją
zbioru B) i jest dany wzorem:

dla dowolnego 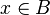 .
.
Algebry wolne
Algebra Boole'a  jest wolna, jeśli pewien zbiór
jest wolna, jeśli pewien zbiór  ma następującą własność:
ma następującą własność:
- dla każdej algebry Boole'a
 i każdego odwzorowania
i każdego odwzorowania 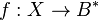 istnieje dokładnie jeden homomorfizm
istnieje dokładnie jeden homomorfizm  z algebry
z algebry  w algebrę
w algebrę  , przedłużający
, przedłużający  (czyli taki, że
(czyli taki, że  ).
).
Zbiór  o własności opisanej powyżej jest nazywany zbiorem wolnych generatorów algebry
o własności opisanej powyżej jest nazywany zbiorem wolnych generatorów algebry  . Jeśli
moc zbioru
. Jeśli
moc zbioru
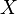 jest
jest 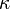 , to mówimy, że
, to mówimy, że  jest wolną algebrą Boole'a z
jest wolną algebrą Boole'a z 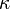 generatorami.
generatorami.
Skończona
algebra Boole'a jest wolna wtedy i tylko wtedy, gdy ma ona  elementów (dla
elementów (dla  ). Algebra mocy
). Algebra mocy  jest izomorficzna z ciałem wszystkich podzbiorów zbioru z
jest izomorficzna z ciałem wszystkich podzbiorów zbioru z 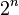 elementami i jako taka ma
elementami i jako taka ma  wolnych generatorów.
wolnych generatorów.
Nieskończona przeliczalna
algebra Boole'a jest wolna wtedy i tylko wtedy, gdy jest bezatomowa, tzn. każdy niezerowy element algebry zawiera przynajmniej dwa różne niezerowe elementy algebry. W zapisie formalnym: 
Zupełne algebry Boole'a
Działania nieskończone
Ponieważ w algebrze Boole'a istnieje porządek częściowy, to dla zbioru 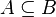 można rozpatrywać jego
kresy
(które istnieją lub nie).
można rozpatrywać jego
kresy
(które istnieją lub nie).
Jeśli dwuczłonowe operacje algebry Boole'a są oznaczane przez  (tak jak w tym artykule), to kres górny zbioru
(tak jak w tym artykule), to kres górny zbioru  (gdy istnieje) jest oznaczany przez
(gdy istnieje) jest oznaczany przez  , a jego kres dolny (gdy istnieje) jest oznaczany przez
, a jego kres dolny (gdy istnieje) jest oznaczany przez  . Jeśli natomiast symbolami dla tych operacji są
. Jeśli natomiast symbolami dla tych operacji są  , to kresy oznaczane są przez
, to kresy oznaczane są przez  ,
,  .
.
Dla zbioru pustego:
 oraz
oraz  .
.
Zakładając istnienie odpowiednich kresów, zachodzą wzory de Morgana:
 oraz
oraz 
Ponadto, jeśli  , to:
, to:
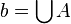 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
 oraz
oraz ,
,
 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
 oraz
oraz .
.
Zupełność
Następujące dwa stwierdzenia są równoważne dla algebry Boole'a  :
:
- każdy podzbiór
 ma kres górny;
ma kres górny; - każdy podzbiór
 ma kres dolny.
ma kres dolny.
Algebry, w których każdy zbiór ma kres górny (tzn. takie dla których porządek boole'owski  jest
zupełny
), są nazywane zupełnymi algebrami Boole'a. Zupełne algebry Boole'a są szczególnie ważne w teorii
forsingu
; są one też przykładami
krat zupełnych
.
jest
zupełny
), są nazywane zupełnymi algebrami Boole'a. Zupełne algebry Boole'a są szczególnie ważne w teorii
forsingu
; są one też przykładami
krat zupełnych
.
Niech 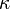 będzie
liczbą kardynalną
, a
będzie
liczbą kardynalną
, a  będzie algebrą Boole'a. Powiemy, że algebra
będzie algebrą Boole'a. Powiemy, że algebra  jest κ-zupełna, jeśli każdy zbiór
jest κ-zupełna, jeśli każdy zbiór 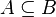 mocy mniejszej niż
mocy mniejszej niż 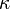 ma kres górny (tzn.
ma kres górny (tzn.  istnieje ilekroć
istnieje ilekroć  ). Równoważnie: algebra
). Równoważnie: algebra  jest
jest 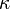 -zupełna wtedy i tylko wtedy, gdy każdy zbiór
-zupełna wtedy i tylko wtedy, gdy każdy zbiór 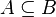 , o mocy mniejszej niż
, o mocy mniejszej niż 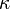 , ma kres dolny (tzn
, ma kres dolny (tzn  ). Algebry
). Algebry  -zupełne są też nazywane algebrami σ-zupełnymi.
-zupełne są też nazywane algebrami σ-zupełnymi.
Jeśli 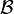 jest σ-
ciałem
borelowskich
podzbiorów
prostej rzeczywistej
(a więc jest to σ-zupełna algebra Boole'a) oraz
jest σ-
ciałem
borelowskich
podzbiorów
prostej rzeczywistej
(a więc jest to σ-zupełna algebra Boole'a) oraz 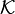 , jest rodziną wszystkich zbiorów
, jest rodziną wszystkich zbiorów 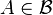 , które są
pierwszej kategorii
, to
, które są
pierwszej kategorii
, to 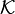 jest ideałem w algebrze
jest ideałem w algebrze 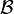 i algebra ilorazowa
i algebra ilorazowa 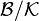 jest zupełna. Podobnie dla rodziny
jest zupełna. Podobnie dla rodziny 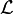 wszystkich borelowskich
zbiorów miary zero
.
wszystkich borelowskich
zbiorów miary zero
.
Zbiory niezależne
Podzbiór X algebry Boole'a  nazywany jest niezależnym, gdy dla dowolnych zbiorów skończonych
nazywany jest niezależnym, gdy dla dowolnych zbiorów skończonych 
 .
.
Do klasycznych twierdzeń dotyczących zbiorów niezależnych w algebrach Boole'a należą:
Funkcje kardynalne
W badaniach i opisach algebr Boole'a często używa się
funkcji kardynalnych
. Przykładami takich funkcji kardynalnych są następujące funkcje.
- Celularność
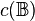 algebry Boole'a
algebry Boole'a  jest to supremum mocy
antyłańcuchów
w
jest to supremum mocy
antyłańcuchów
w  .
. - Długość
 algebry Boole'a
algebry Boole'a  to
to
 jest
łańcuchem
jest
łańcuchem

- Głębokość
 algebry Boole'a
algebry Boole'a  to
to
 jest
dobrze uporządkowanym
łańcuchem
jest
dobrze uporządkowanym
łańcuchem  .
.
- Nieporównywalność
 algebry Boole'a
algebry Boole'a  to
to
 oraz
oraz  .
.
- Pseudo-ciężar
 algebry Boole'a
algebry Boole'a  to
to
 oraz
oraz  .
.
Reprezentacja
Twierdzenie Stone'a o reprezentacji algebr Boole'a
mówi, że każda algebra Boole'a jest izomorficzna z pewnym ciałem zbiorów (traktowanym jako algebra Boole'a). Dokładniej mówiąc, algebra Boole'a  jest izomorficzna z ciałem
otwarto-domkniętych
podzbiorów przestrzeni
ultrafiltrów
na
jest izomorficzna z ciałem
otwarto-domkniętych
podzbiorów przestrzeni
ultrafiltrów
na  , tzw.
przestrzeni Stone'a
algebry
, tzw.
przestrzeni Stone'a
algebry  . Twierdzenie Stone'a nie może być udowodnione przy użyciu tylko
ZF
– wymaga ono założenia pewnej formy
aksjomatu wyboru
(rozszerzalności ideałów w algebrach Boole'a do ideałów pierwszych).
. Twierdzenie Stone'a nie może być udowodnione przy użyciu tylko
ZF
– wymaga ono założenia pewnej formy
aksjomatu wyboru
(rozszerzalności ideałów w algebrach Boole'a do ideałów pierwszych).
Każda skończona algebra Boole'a jest izomorficzna z całym
zbiorem potęgowym
 dla pewnego
dla pewnego 
Historia
Nazwa „algebra Boole'a” pochodzi od nazwiska
George'a Boole'a
(
1815
–
1864
), angielskiego matematyka-samouka. Wprowadził on algebraiczne ujęcie
logiki matematycznej
w niewielkiej pracy The Mathematical Analysis of Logic (Matematyczna analiza logiki), opublikowanej w 1847 roku. W późniejszej książce The Laws of Thought (Prawa myśli), opublikowanej w 1854, Boole formułuje problem w bardziej dojrzały sposób, zauważając dualność operacji ∪ i ∩. Dalszy rozwój algebra Boole'a zawdzięcza Williamowi Jevonsowi i
Charlesowi Peirce'owi
, których prace opublikowane zostały w latach sześćdziesiątych XIX wieku. W 1890 w Vorlesungen (Wykłady)
Ernsta Schrödera
pojawia się pierwszy systematyczny wykład algebry Boole'a i krat rozdzielnych. Dokładniejsze badania algebr Boole'a podjął
Alfred North Whitehead
w wydanym w 1898 roku dziele Universal Algebra (Algebra ogólna). Algebra Boole'a jako aksjomatyczna struktura algebraiczna pojawiła się w 1904 roku w pracach Huntingtona. Garrett Birkhoff w Lattice Theory (1940) rozwinął teorię krat. W latach sześćdziesiątych
Paul Cohen
,
Dana Scott
i inni osiągnęli głębokie rezultaty w dziedzinie logiki matematycznej i aksjomatycznej teorii zbiorów, korzystając z metody
forsingu
osadzonej w teorii algebr Boole'a.
Pierścienie Boole'a
Z pojęciem algebry Boole'a związane jest pojęcie pierścienia Boole'a. Pierścień Boole'a to
pierścień przemienny
z jedynką  , w którym mnożenie spełnia warunek
, w którym mnożenie spełnia warunek
 dla każdego elementu
dla każdego elementu  .
.
W pierścieniu Boole'a każdy element jest rzędu 2, to znaczy spełnia równość:  . Dowód:
. Dowód:
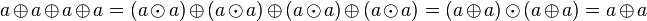
więc  .
.
Wynika stąd, że:
 oraz
oraz  .
.
Niech  będzie algebrą Boole'a. Jeżeli w zbiorze
będzie algebrą Boole'a. Jeżeli w zbiorze 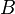 określi się operację
różnicy symetrycznej
określi się operację
różnicy symetrycznej
 przez
przez

to  będzie pierścieniem Boole'a; za mnożenie
będzie pierścieniem Boole'a; za mnożenie  przyjmuje się
przyjmuje się  .
.
I na odwrot – niech  będzie pierścieniem Boole'a. Jeżeli zdefiniuje się operacje
będzie pierścieniem Boole'a. Jeżeli zdefiniuje się operacje  i ˜ na
i ˜ na 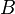 przez
przez
 ,
,  i
i  ,
,
to  będzie algebrą Boole'a spełniającą
będzie algebrą Boole'a spełniającą

Bibliografia
- Zofia Adamowicz, Paweł Zbierski: Logic of mathematics. A modern course of classical logic. Nowy Jork: A Wiley-Interscience Publication. John Wiley & Sons, Inc., 1997, seria: Pure and Applied Mathematics. .
- Garrett Birkhoff, Thomas C. Bartee: Współczesna algebra stosowana. Warszawa: Państwowe Wydawnictwo Naukowe, 1983, seria: Matematyka dla Politechnik. .
-
Thomas Jech
: Set theory. Berlin: Springer-Verlag, 1997. .
- Winfried Just, Martin Weese: Discovering modern set theory. T. 2: Set-theoretic tools for every mathematician. Providence, RI:
American Mathematical Society
, 1997. .
- Sabine Koppelberg: Handbook of Boolean algebras. J. Donald Monk i Robert Bonnet (red.). T. 1,2,3. Amsterdam: North-Holland Publishing Co., 1989. .
-
Kazimierz Kuratowski
,
Andrzej Mostowski
: Teoria mnogości: wraz ze wstępem do opisowej teorii mnogości. Wyd. 3. Warszawa: Państwowe Wydawnictwo Naukowe (PWN), 1978, seria: Monografie Matematyczne 27.
- J. Donald Monk: Cardinal invariants on Boolean algebras. Basel: Birkhäuser Verlag, 1996. .
-
Helena Rasiowa
: Wstęp do matematyki współczesnej. Warszawa: Państwowe Wydawnictwo Naukowe, 1973, seria: Biblioteka Matematyczna t. 30.
-
Roman Sikorski
: Boolean Algebras (wydanie 3). Springer Verlag; Ergebnisse der Mathematik und ihrer Grenzgebieterok. Neue Folge. Band 25, 1969 (wyd. 1 – 1960).
Zobacz też
Wystąpił problem z bazą danych.
Spróbuj ponownie poprzez naciśnięcie przycisku "Odśwież".
Przepraszamy za powstały problem.