Średnią arytmetyczną liczb nazywamy liczbę: Inaczej mówiąc jest to iloraz sumy n liczb i n (gdzie n to ilość sumowanych liczb).

Przykłady zastosowania

Średnia arytmetyczna jest właśnie tym, co w potocznym języku określa się mianem średniej. Można ją również określić jako średnią potęgową rzędu 1.

Na przykład średnią liczb -5,-3, 0 i 12 jest

Średnia arytmetyczna jest jedną z najbardziej intuicyjnych miar oceny populacji, stosowanych często w codziennym życiu – przykładem może być średnia ocen z matematyki ucznia szkoły podstawowej, który otrzymał następujące noty: 2, 4, 4, 5, 6

W podobny sposób można mówić o średniej płacy w danej firmie, średniej cenie pomarańczy na targowiskach w lipcu 2004 roku czy średnim wzroście poborowych w danym roczniku. Czasami jednak, w próbach o rozkładzie dalekim od normalnego z dużym udziałem obserwacji odstających lepszą miarą jest mediana .

Średnia arytmetyczna jest dobrą miarą położenia rozkładu i jednocześnie miarą tendencji centralnej . Jest to miara klasyczna rozkładu , czyli każda zmiana dowolnego elementu badanego zbioru pociąga za sobą zmianę wartości średniej.

Właściwości statystyczne średniej z próby

Odchylenie standardowe średniej

Jeśli uśredniamy nieskorelowanych ^[1] zmiennych o odchyleniach standardowych , to odchylenie ich średniej arytmetycznej jest równe średniej kwadratowej odchyleń tych zmiennych:

Jeśli zmienne są skorelowane, wówczas odchylenie średniej będzie inne, np. dla dwóch zmiennych :

gdzie 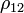to współczynnik korelacji między nimi.

W ogólnym przypadku dla skorelowanych zmiennych:

gdzie to kowariancja i-tej i j-tej zmiennej.

Prawo wielkich liczb

Niech będzie zmienną losową o skończonej wariancji i wartości oczekiwanej oraz niech 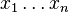będzie prostą próbą losową z tej zmiennej. Wtedy dla dowolnie małej dodatniej liczby :

Innymi słowy średnia próbkowa dąży do wartości oczekiwanej w populacji wraz ze wzrostem liczności próby. Prawo wielkich liczb można wzmocnić na dwa sposoby, przedstawione dalej.

Centralne twierdzenie graniczne

Zgodnie z centralnym twierdzeniem granicznym rozkład średniej z n-elementowej próby wraz ze wzrostem n coraz lepiej odpowiada rozkładowi normalnemu o wartości oczekiwanej i odchyleniu , gdzie oraz 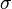to odpowiednio wartość oczekiwana oraz odchylenie standardowe w populacji, z której losowana jest próba. Ściślej dla dowolnych liczb rzeczywistych takich, że :

gdzie:

• to zmienna o standardowym rozkładzie normalnym (o wartości oczekiwanej zero i wariancji równej jeden),
• to dystrybuanta rozkładu normalnego

Twierdzenie to jest prawdziwe niezależnie od rozkładu w populacji. Właściwość ta jest wykorzystywana w wielu metodach statystycznych i estymatorach . Centralne twierdzenie graniczne jest uogólnieniem prawa wielkich liczb, gdyż opisuje zachowanie całego rozkładu średniej, podczas gdy prawo wielkich liczb opisywało jeden jego parametr (wartość oczekiwaną).

Właściwości średniej jako estymatora

Średnia arytmetyczna w próbie jest, niezależnie od rozkładu, estymatorem zgodnym i nieobciążonym wartości oczekiwanej rozkładu, z którego próba była losowana. Jeśli jest to rozkład normalny , to średnia jest również estymatorem efektywnym .

Ograniczenia

Średnia arytmetyczna jest podatna na obserwacje odstające (czyli w tym przypadku wartości zmiennej, losowane spoza rozkładu, którego wartość oczekiwaną chcemy estymować, np. pomyłki w danych). W przypadku gdy jest ich dostatecznie dużo, inne średnie , takie jak mediana czy średnia ucinana , mogą dawać lepsze wyniki.

Przypisy

Bibliografia

• Jacek Koronacki, Jan Mielniczuk: Statystyka dla studentów kierunków technicznych i przyrodniczych. Warszawa: WNT, 2001. . 
• W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska, M. Wasilewski: Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach, część 2. Statystyka matematyczna. Warszawa: PWN, 2006, s. 48. . 

Zobacz też

• nierówność Cauchy'ego o średnich
• nierówność między średnimi potęgowymi
• centralne twierdzenie graniczne