|
|
|
Zbiór stacjonarny
Zbiór stacjonarnyW
teorii mnogości
, zbiory stacjonarne i cluby to podzbiory
liczb kardynalnych
(traktowanych jako
liczby porządkowe
) które są w pewnym sensie duże. DefinicjeNiech κ będzie
nieprzeliczalną
regularną
liczbą
kardynalną
(która będziemy traktować jako początkową liczbę porządkową). - Powiemy, że zbiór
 jest domknięty jeśli jest on
domknięty
w topologii porządkowej na κ, który to warunek jest równoważny stwierdzeniu, że dla każdej
granicznej
liczby α < κ mamy jest domknięty jeśli jest on
domknięty
w topologii porządkowej na κ, który to warunek jest równoważny stwierdzeniu, że dla każdej
granicznej
liczby α < κ mamy
 . .- Zbiór
 jest nieograniczony w κ jeśli jest nieograniczony w κ jeśli 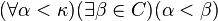 . . - Powiemy, że zbiór
 jest clubem w κ jeśli jest on zarówno domknięty jak i nieograniczony. jest clubem w κ jeśli jest on zarówno domknięty jak i nieograniczony. - Zbiór
 jest stacjonarnym podzbiorem κ, jeśli jest stacjonarnym podzbiorem κ, jeśli  dla każdego domkniętego nieograniczonego (tzn cluba) zbioru dla każdego domkniętego nieograniczonego (tzn cluba) zbioru  . . - Zbiór
 jest niestacjonarnym podzbiorem κ, jeśli S nie jest stacjonarny, czyli gdy jest niestacjonarnym podzbiorem κ, jeśli S nie jest stacjonarny, czyli gdy  dla pewnego cluba dla pewnego cluba  . .
Nazwa club jest skrótem
angielskiego
terminu closed and unbounded. Niektórzy autorzy używają też nazwy c.u.b. (np taka nazwa używana jest w
monografii
Kunena[1]) Własności i przykładyNiech κ będzie nieprzeliczalną regularną liczbą kardynalną. - Zbiór wszystkich granicznych liczb porządkowych mniejszych niż κ jest clubem, podobnie jak i zbiór wszystkich granic liczb granicznych.
- Zbiór wszystkich granicznych liczb porządkowych α < κ o przeliczalnej współkońcowości jest stacjonarnym podzbiorem κ.
- Dla każdej
funkcji
 , zbiór , zbiór  jest clubem w κ. jest clubem w κ. - Jeśli
 jest
rodziną
clubów na κ, jest
rodziną
clubów na κ,  , to
przekrój , to
przekrój
 też jest clubem. też jest clubem. - Z powyższej obserwacji wynika, że rodzina
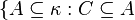 dla pewnego cluba dla pewnego cluba  - jest κ-zupełnym
filtrem
podzbiorów κ.
- Rodzina
 wszystkich niestacjonarnych podzbiorów κ tworzy κ-zupełny
ideał
podzbiorów κ. wszystkich niestacjonarnych podzbiorów κ tworzy κ-zupełny
ideał
podzbiorów κ.
- Lemat Fodora mówi, że jeśli S jest stacjonarnym podzbiorem κ oraz
 jest funkcją taką że jest funkcją taką że 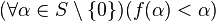 , to funkcja f jest
stała
na pewnym stacjonarnym podzbiorze zbioru S. (Odwrotnie, jeśli S jest niestacjonarnym podzbiorem κ, to istnieje funkcja , to funkcja f jest
stała
na pewnym stacjonarnym podzbiorze zbioru S. (Odwrotnie, jeśli S jest niestacjonarnym podzbiorem κ, to istnieje funkcja  taka że taka że 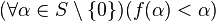 która nie jest stała na żadnym nieograniczonym podzbiorze zbioru S.) która nie jest stała na żadnym nieograniczonym podzbiorze zbioru S.)
Bibliografia- ↑ Kunen, Kenneth. Set theory. An introduction to independence proofs. Studies in Logic and the Foundations of Mathematics, 102. North-Holland Publishing Co., Amsterdam-New York, 1980. xvi+313 pp.
Zobacz też
Inne hasła zawierające informacje o "Zbiór stacjonarny":
Trzcina cukrowa
...
Sortowanie
...
Grupa
...
Tomasz Zan (poeta)
...
Świadomość społeczna
...
Samuel Johnson
...
Musical
...
Rekultywacja jezior
...
Konstanty Fredro
...
Jarząb pospolity
...
Inne lekcje zawierające informacje o "Zbiór stacjonarny":
Zbiory liczbowe (plansza 14)
...
Algorytmy sortujące - sortowanie przez wstawianie, sortowanie przez wybór (plansza 3)
...
Algorytmy sortujące - sortowanie bąbelkowe, część II (plansza 3)
...
|
|
|
|