Wyznacznik – w algebrze liniowej , funkcja przyporządkowująca każdej macierzy kwadratowej M, o współczynnikach z pierścienia przemiennego R (w szczególności, ciała liczb rzeczywistych czy zespolonych ), pewien element tego pierścienia (oznaczany symbolem detM), która spełnia następujące warunki:

1. wartością tej funkcji na macierzy 1x1 [a] jest a,
2. jeśli

jest macierzą kwadratową stopnia n>1, to wartość tej funkcji dla macierzy M równa się

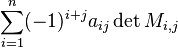, gdzie j jest dowolną liczbą naturalną z zakresu 1 <= j <= n, a przez M_i,j oznaczamy macierz stopnia n-1, powstałą z macierzy M poprzez skreślenie i-tego wiersza i j-tej kolumny (por. minor ).

Funkcja o powyższych własnościach wyznaczona jest jednoznacznie. Wyznacznikiem macierzy M nazywamy wartość detM tej funkcji dla macierzy M.

Wyznacznik można również traktować jako funkcję, nie samej macierzy, a jej współczynników

.

Jest on wówczas wielomianem n² zmiennych o współczynnikach z R.

Zapis

Wyznacznik macierzy kwadratowej M oznaczany jest czasami przez | M | . Ta notacja może jednak prowadzić do nieporozumień, ponieważ używa się jej do zapisu norm macierzy lub wartości bezwzględnej . Zapis z użyciem pionowych kresek jest jednak szeroko rozpowszechniony w matematyce.

Dla macierzy

wprowadzamy oznaczenie

.

Rozwinięcie Laplace'a

Istnieje jeszcze jeden (równoważny) sposób wprowadzenia pojęcia wyznacznika (zob. definicja permutacyjna poniżej), jednak tak wprowadzona definicja (tzw. definicja rekurencyjna wyznacznika) ukazuje efektywną metodę obliczania wyznaczników macierzy kwadratowych wyższych stopni. W szczególności, prawdziwe jest następujące twierdzenie Laplace'a:

Jeżeli M jest macierzą taką jak wyżej oraz i jest liczbą naturalną nie większą niż n, to zachodzą równości

. (rozwinięcie wyznacznika względem i-tego wiersza)

oraz

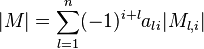. (rozwinięcie wyznacznika względem i-tej kolumny).

Definicja permutacyjna

Jeżeli M jest macierzą taką, jak wyżej, to

,

gdzie S_n oznacza zbiór wszystkich permutacji zbioru , zaś Inv(σ) oznacza liczbę inwersji danej permutacji .

Przykładowo składnik a₁₃a₂₁a₃₄a₄₂ w wyznaczniku czwartego stopnia ma ujemny znak, gdyż permutacja indeksów

,

ma trzy inwersje, mianowicie: (3,1), (3,2) i (4,2), skąd Inv(τ) = 3 oraz ( − 1)³ = − 1.

Wyznacznik ogólny

Wyznacznikiem ogólnym z parametrem p nazywamy:

,

gdzie M, S_n, Inv(σ) jak wyżej.

Przykładowo dla p = − 1 otrzymujemy wyznacznik, zaś dla p = 1 otrzymujemy permanent .

Definicja wyznacznika jako odwzorowania wieloliniowego

Jeżeli macierz potraktujemy jako ciąg n kolumn (każda kolumna to element z przestrzeni liniowej ), to istnieje dokładnie jedno antysymetryczne odwzorowanie wieloliniowe takie, że det(I) = 1. Wartość odwzorowania det(A) nazywamy wyznacznikiem macierzy A.

Własności

1. Transpozycja macierzy nie powoduje zmiany wartości jej wyznacznika.
2. Zamiana miejscami dwóch dowolnych kolumn lub wierszy zmienia znak wyznacznika, nie zmieniając jego wartości bezwzględnej.
3. Jeśli dwa wiersze lub dwie kolumny macierzy są proporcjonalne (np. są równe), wyznacznik ma wartość zero.
4. Jeśli jakiś wiersz jest kombinacją liniową innych wierszy (np. wiersz składa się tylko z zer), wyznacznik ma wartość zero. To samo dotyczy kolumn.
5. Pomnożenie dowolnej kolumny lub dowolnego wiersza przez stałą mnoży przez tę samą stałą wartość wyznacznika.
6. Dodając lub odejmując od dowolnego wiersza/kolumny inny wiersz/kolumnę lub kombinacje liniowe innych wierszy/kolumn nie zmieniamy wartości wyznacznika.
7. Rozwinięcie Laplace'a — wyznacznik stopnia n można rozłożyć według i-tego wiersza zgodnie ze wzorem
   
   detA = a_i1A_i1 + a_i2A_i2 + ... + a_inA_in
   
   gdzie A_ij jest dopełnieniem algebraicznym elementu a_ij, czyli wyznacznikiem macierzy, powstałej po skreśleniu i-tego wiersza oraz j-tej kolumny, pomnożonym przez ( − 1)^{j + i}. Analogiczny wzór obowiązuje dla kolumn.
8. Wyznacznik iloczynu macierzy jest równy iloczynowi wyznaczników: .
9. Wyznacznik macierzy odwrotnej jest równy odwrotności wyznacznika: det(A ^{− 1}) = (detA) ^{− 1}.
10. Zachodzi , gdzie k jest dowolną liczbą, n stopniem macierzy A.

Obliczanie wyznaczników

Wyznacznik drugiego stopnia obliczamy według łatwego wzoru, wynikającego wprost z definicji permutacyjnej wyznacznika:

Wyznacznik trzeciego stopnia obliczamy według tzw. reguły Sarrusa :

W przypadku macierzy wyższych stopni, a także niejednokrotnie w przypadku macierzy stopnia trzeciego, wygodniej jest stosować twierdzenie Laplace'a . Przykład obliczenia wyznacznika czwartego stopnia znajduje się we wspomnianym artykule .

Wyznacznik macierzy można też obliczyć stosując metodę eliminacji Gaussa . Wyznacznik macierzy trójkątnej jest równy iloczynowi wyrazów na jej przekątnej, jest więc łatwy do obliczenia. Każdą macierz można sprowadzić do macierzy trójkątnej za pomocą operacji elementarnych, pamiętając że operacje te mają następujący wpływ na wyznacznik:

1. Dodanie wielokrotności jednego wiersza (kolumny, odpowiednio) do innego wiersza (innej kolumny, odpowiednio) nie zmienia wartości wyznacznika;
2. Pomnożenie wiersza (kolumny) przez liczbę powoduje pomnożenie wyznacznika przez tę liczbę;
3. Zamiana miejscami dwóch wierszy, tak jak i zamiana miejscami dwóch kolumn, zmienia znak wyznacznika.

Do obliczenia wyznacznika można wykorzystać również metodę LU .

Zastosowanie wyznaczników

Wyznaczniki pojawiają się w wielu miejscach w matematyce, np. przy:

• rozwiązywaniu układów równań liniowych ,
• odwracaniu macierzy ,
• obliczaniu objętości brył (np. czworościanu ), a więc m.in. w analizie ,
• badaniu wielomianu Hurwitza (stabilność systemu),
• zamianie zmiennych w całkach wielokrotnych
• do sprawdzenia czy punkt znaleziony w zadaniu ekstremalnym jest minimum czy maksimum z kryterium Sylwestera ,

i w wielu, wielu innych miejscach.

Dowody niektórych własności

Przyjmijmy następujące własności wyznacznika:

• pomnożenie kolumny przez x mnoży wyznacznik macierzy przez x
• dodanie jednej kolumny do drugiej nie zmienia wartości wyznacznika

Ponieważ bardzo wiele operacji można zbudować z mnożeń przez stałą i dodawań kolumn (wierszy), możemy z tych dwóch właściwości wyprowadzić wiele innych własności.

W poniższych przykładach będziemy budować kolejno macierze M¹, M², M³ itd., a przez aⁱ,bⁱ,cⁱ będziemy oznaczać pewne kolumny i-tej macierzy. Wszystkie kolumny o których nic nie powiedziano są takie same jak w poprzedniej macierzy.

Odjęcie jednej kolumny od drugiej nie zmienia wartości wyznacznika:

1. Zamieńmy znak w kolumnie a:

   a² = − a¹.

   b² = b¹

   detM² = − detM¹

2. Dodajmy kolumnę a do kolumny b:

   a³ = a² = − a¹.

   b³ = b² + a² = b¹ − a¹

   detM³ = detM² = − detM¹

3. Zamieńmy ponownie znak w kolumnie a:

   a⁴ = − a³ = a¹.

   b⁴ = b³ = b¹ − a¹

   detM⁴ = − detM³ = detM¹

Dodanie dowolnej wielokrotności jednej kolumny do drugiej nie zmienia wartości wyznacznika:

1. Pomnóżmy kolumnę a przez x:

   a² = xa¹.

   b² = a¹

   detM² = xdetM¹

2. Dodajmy kolumnę a do kolumny b:

   a³ = a² = xa¹.

   b³ = b² + a² = b¹ + xa¹

   detM³ = detM² = xdetM¹

3. Pomnóżmy kolumnę a przez :

   .

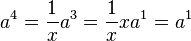   b⁴ = b³ = b¹ + xa¹

   

W powyższym przykładzie założyliśmy, że istnieje odwrotność x, a zatem x jest różne od 0. Jeśli x jest równe 0, dodanie 0 razy kolumna to kolumna złożona z samych zer, a dodanie kolumny zer do innej kolumny nie zmienia macierzy, więc wyznacznik pozostaje ten sam.

Zamiana dwóch kolumn miejscami zmienia znak wyznacznika:

1. Dodajmy kolumnę a do kolumny b:

   a² = a¹.

   b² = a¹ + b¹

   detM² = detM¹

2. Zamieńmy znak w kolumnie a:

   a³ = − a² = − a¹.

   b³ = b² = a¹ + b¹

   detM³ = − detM² = − detM¹

3. Dodajmy kolumnę b do kolumny a:

   a⁴ = a³ + b³ = − a¹ + a¹ + b¹ = b¹.

   b⁴ = b³ = a¹ + b¹

   detM⁴ = detM³ = − detM¹

4. Zamieńmy znak w kolumnie b:

   a⁵ = a⁴ = b¹.

   b⁵ = − b⁴ = − a¹ − b¹

   detM⁵ = − detM⁴ = detM¹

5. Dodajmy kolumnę a do kolumny b:

   a⁶ = a⁵ = b¹.

   b⁶ = a⁵ + b⁵ = b¹ − a¹ − b¹ = − a¹

   detM⁶ = detM⁵ = detM¹

6. Zamieńmy znak w kolumnie b:

   a⁷ = a⁶ = b¹.

   b⁷ = − b⁶ = a¹

   detM⁷ = − detM⁶ = − detM¹

Po tej serii operacji (którą można uprościć korzystając z udowodnionej wyżej własności, że odejmowanie kolumn nie zmienia wyznacznika), wartości w kolumnach a i b zamieniły się miejscami, a wyznacznik zmienił znak.

Analogicznie wyprowadza się te zależności dla wierszy.

Zobacz też

• ,
• permanent ,
• tensor ,
• tensor alternujący,
• twierdzenie Cauchy'ego (teoria wyznaczników) ,
• wrońskian , hesjan , jakobian ,
• metoda Gaussa ,
• metoda LU .

Linki zewnętrzne

• Skrypt liczący m.in. wyznacznik macierzy