|
Zbiór miary zero
Zbiór miary zeroZbiory miary zero – w
analizie matematycznej
,
teorii mnogości
, a przede wszystkim w
teorii miary
podzbiory rozważanej przestrzeni, które są „małe” lub z punktu widzenia
miary
. DefinicjeNiech  będzie
przestrzenią z miarą
.
Podzbiór
A przestrzeni X nazywany jest zbiorem μ-miary zero (lub krótko: zbiorem miary zero, jeśli z kontekstu wynika o jaką miarę chodzi), gdy będzie
przestrzenią z miarą
.
Podzbiór
A przestrzeni X nazywany jest zbiorem μ-miary zero (lub krótko: zbiorem miary zero, jeśli z kontekstu wynika o jaką miarę chodzi), gdy - A jest
 -mierzalny, tzn. -mierzalny, tzn. 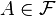  . .
Podzbiory zbiorów miary zero (które nie muszą być mierzalne w przypadku miar, które nie są
miara zupełna
) nazywa się zbiorami zaniedbywalnymi (w sensie rozważanej miary). Jeżeli miara nie jest sprecyzowana, to dla
przestrzeni euklidesowej
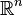 przyjmuje się domyślnie
miarę Lebesgue'a
λn, z kolei gdy dyskutowana przestrzeń jest
lokalnie zwartą
grupą topologiczną
, to na ogół mówi się o zbiorach miary zero względem (lewostronnie niezmienniczej)
miary Haara
. przyjmuje się domyślnie
miarę Lebesgue'a
λn, z kolei gdy dyskutowana przestrzeń jest
lokalnie zwartą
grupą topologiczną
, to na ogół mówi się o zbiorach miary zero względem (lewostronnie niezmienniczej)
miary Haara
. Mówi się, że pewna własność zachodzi prawie wszędzie, jeżeli zbiór punktów nie mających tej własności jest zbiorem miary zero (względem ustalonej miary). PrzykładNiech  na przestrzeni na przestrzeni  , wówczas , wówczas  są równe prawie wszędzie wtedy i tylko wtedy, gdy zbiór są równe prawie wszędzie wtedy i tylko wtedy, gdy zbiór 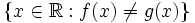 jest zbiorem miary zero, jest zbiorem miary zero,- ciąg (fk)k jest prawie wszędzie zbieżny do f wtedy i tylko wtedy, gdy zbiór
 jest zbiorem miary zero, jest zbiorem miary zero, - f jest ciągła prawie wszędzie wtedy i tylko wtedy, gdy zbiór
 nie jest ciągła w punkcie nie jest ciągła w punkcie  jest zbiorem miary zero. jest zbiorem miary zero.
Zbiory miary zero Lebesgue'aW przypadku miary Lebesgue'a, możemy zdefiniować zbiory miary zero bez odwoływania się bezpośrednio do pojęcia miary. Niech 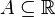 . Powiemy, że A jest zbiorem miary zero (w sensie Lebesgue'a), jeśli dla każdego . Powiemy, że A jest zbiorem miary zero (w sensie Lebesgue'a), jeśli dla każdego  można wybrać taki ciąg
odcinków
otwartych można wybrać taki ciąg
odcinków
otwartych  , że , że 
oraz  . .
Powyżej, dla odcinka otwartego I = (a,b), długość odcinka I wynosi | I | = b − a. Jeśli rozważaną przestrzenią jest 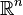 , to zamiast odcinków używamy tzw.
przedziałów wielowymiarowych
, czyli kostek otwartych – zbiorów postaci , to zamiast odcinków używamy tzw.
przedziałów wielowymiarowych
, czyli kostek otwartych – zbiorów postaci  , gdzie , gdzie  są przedziałami otwartymi oraz są przedziałami otwartymi oraz  . .
Przykłady i własnościNiech  będzie rodziną wszystkich podzbiorów
prostej rzeczywistej
, które są miary zero Lebesgue'a. będzie rodziną wszystkich podzbiorów
prostej rzeczywistej
, które są miary zero Lebesgue'a. - Trójkowy
klasyczny zbiór Cantora
jest zbiorem miary zero. Należy jednak podkreślić, że nie wszystkie zbiory Cantora mają tę własność – poprzez odpowiednie zmiany w konstrukcji (wyrzucanie odpowiednio mniejszych odcinków) możemy skonstruować zbiór Cantora dowolnej skończonej miary.
- Prostą rzeczywistą
 można przedstawić jako
sumę
dwóch zbiorów, można przedstawić jako
sumę
dwóch zbiorów, 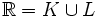 , takich że , takich że  , a K jest
zbiorem pierwszej kategorii
. , a K jest
zbiorem pierwszej kategorii
.- Aby podać przykład takich zbiorów
 ustalmy numerację ustalmy numerację  zbioru liczb wymiernych (przypomnijmy, że zbiór liczb wymiernych jest
przeliczalny
). Dla zbioru liczb wymiernych (przypomnijmy, że zbiór liczb wymiernych jest
przeliczalny
). Dla  , niech , niech  będzie odcinkiem otwartym o środku w qn i długości 2 − (n + m). Wówczas zbiór będzie odcinkiem otwartym o środku w qn i długości 2 − (n + m). Wówczas zbiór  jest miary zero, ale jego
dopełnienie jest miary zero, ale jego
dopełnienie
 jest pierwszej kategorii. jest pierwszej kategorii.
- Inny przykład rozkładu jak powyżej jest dany przez
liczby Liouville'a
: zbiór liczb Liouville'a jest miary zero na prostej, a jego dopełnienie jest zbiorem pierwszej kategorii.
 jest
σ-ideałem podzbiorów
prostej. Zawiera on wszystkie zbiory jednopunktowe, a więc także i wszystkie
zbiory przeliczalne
. jest
σ-ideałem podzbiorów
prostej. Zawiera on wszystkie zbiory jednopunktowe, a więc także i wszystkie
zbiory przeliczalne
.- Każdy zbiór z
 zawarty jest w
zbiorze typu Gδ
należącym do zawarty jest w
zbiorze typu Gδ
należącym do  . . - Każda rodzina rozłącznych
borelowskich
podzbiorów
 , które nie są miary zero (w sensie Lebesgue'a) jest co najwyżej przeliczalna. , które nie są miary zero (w sensie Lebesgue'a) jest co najwyżej przeliczalna. - Konsekwencją
zasady Cavalieriego
jest fakt mówiący, że jeżeli E jest podzbiorem miary zero przestrzeni
 , to , to
 dla prawie wszystkich dla prawie wszystkich 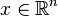 , , dla prawie wszystkich dla prawie wszystkich  . .
- (i)
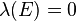 , , - (ii)
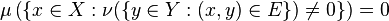 , , - (iii)
 . .
Bibliografia-
Stanisław Łojasiewicz
: Wstęp do teorii funkcji rzeczywistych. Warszawa:
PWN
, 1973, ss. 144-145.
- John C. Oxtoby: Measure and Category: A Survey of the Analogies Between Topological and Measure Spaces. New York - Heidelberg - Berlin: Springer-Verlag, 1980, ss. 2-5.
Zobacz też
Inne hasła zawierające informacje o "Zbiór miary zero":
Biskup
...
Trzcina cukrowa
...
Sortowanie
...
Grupa
...
Tomasz Zan (poeta)
...
Świadomość społeczna
...
Samuel Johnson
...
Musical
...
Rekultywacja jezior
...
Konstanty Fredro
...
Inne lekcje zawierające informacje o "Zbiór miary zero":
Zbiory liczbowe (plansza 14)
...
Wielkości fizyczne i ich jednostki (plansza 3)
...
Kąty (plansza 14)
...
|