Mechanika kwantowa

Zasada nieoznaczoności Heisenberga

Równanie Schrödingera Wstęp Aparat matematyczny Tło Mechanika klasyczna  · Stara teoria kwantów  · Interferencja  · Notacja Diraca  · Hamiltonian Koncepcje podstawowe Stan kwantowy  · Funkcja falowa  · Superpozycja  · Splątanie kwantowe  · Pomiar  · Nieoznaczoność  · Reguła Pauliego  · Dualizm korpuskularno-falowy  · Dekoherencja kwantowa  · Twierdzenie Ehrenfesta  · Tunelowanie Doświadczenia Doświadczenie Younga  · Doświadczenie Davissona-Germera  · Doświadczenie Sterna-Gerlacha  · Eksperymenty testujące twierdzenie Bella  · Doświadczenie Poppera  · Kot Schrödingera  · Problem testowania bomb Elitzura-Vaidmana  · Gumka kwantowa Sformułowania Obraz Schrödingera  · Obraz Heisenberga  · Obraz Diraca  · Mechanika macierzowa  · Suma po historiach Równania Równanie Schrödingera  · Równanie Pauliego  · Równanie Kleina-Gordona  · Równanie Diraca  · Wzór Rydberga Interpretacje de Broglie'a-Bohma  · Świadomość wywyołuje kolaps  · Spójne historie kwantowe  · Kopenhaska  · Statystyczna  · Zmiennych ukrytych  · Wielu światów  · Logika kwantowa  · Popularna  · Stochastyczna  · Transakcjonalna Zagadnienia zaawansowane Informatyka kwantowa  · Teoria rozpraszania  · Kwantowa teoria pola  · Chaos kwantowy Znani uczeni Planck  · Bohr  · Sommerfeld  · Bose  · Kramers  · Heisenberg  · Born  · Jordan  · Pauli  · Dirac  · de Broglie  · Schrödinger  · von Neumann  · Wigner  · Feynman  · Candlin  · Bohm  · Everett  · Bell  · Wien

Równanie Diraca jest podstawowym równaniem w relatywistycznej mechanice kwantowej , sformułowanym przez angielskiego fizyka Paula Diraca w 1928 roku. Spełnia ono taką samą rolę jak równanie Schrödingera w nierelatywistycznej mechanice kwantowej. W opisie relatywistycznym równanie Diraca ma elegancką postać:

gdzie:

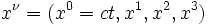- współrzędne punktu w czasoprzestrzeni

- czterogradient

γ^μ

Obiekty γ^μ są czterowymiarowymi macierzami zespolonymi ( macierzami gamma ), są one tak dobrane by spełnione również było równanie Kleina-Gordona . Narzuca to regułę antykomutacyjną postaci:

gdzie:

- antykomutator

Jest bardzo wiele sposobów wyboru tych macierzy, np. reprezentacja Pauliego - Diraca ma postać:

,

σ_i (i=1,2,3) są macierzami Pauliego , zaś I jest macierzą jednostkową.

Ψ(x^ν)

Obiekt Ψ(x^ν) jest nazywany bispinorem Diraca, jest to macierz zespolona pionowa o czterech wierszach:

Bispinor Diraca jest odpowiednikiem funkcji falowej w nierelatywistycznej mechanice kwantowej. Gęstość prawdopodobieństwa w teorii Diraca jest zdefiniowana jako:

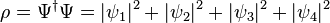
gdzie: oznacza sprzężenie hermitowskie .

Prócz bispinorów i występuje trzeci rodzaj bispinora postaci:

Analogie między równaniem Diraca a Schrödingera

Równanie Diraca można przekształcić do postaci podobnej do równania Schrödingera. Definiujemy nowe macierze:

αⁱ = γ⁰γⁱ

β = γ⁰

Równanie Diraca definiuje hamiltonian relatywistycznego fermionu i przyjmuje postać:

gdzie

i to jednostka urojona

(ha kreślone) jest stałą Plancka podzieloną przez 2π; nazywana niekiedy zredukowaną stałą Plancka lub (zwłaszcza w literaturze anglojęzycznej) stałą Diraca

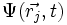jest czteroskładnikową funkcją falową (bispinorem Diraca) zależną od wspołrzędnych czasoprzestrzennych cząstki

c jest prędkością światła

jest operatorem pędu

m₀ masą spoczynkową cząstki

Równanie Diraca pozwala opisywać cząstki o spinie 1/2 ( fermiony ). Gdy cząstka się nie porusza, równanie Diraca przyjmuje postać: