|
Proper forsing
Proper forsingProper forsing (własność proper pojęć forsingu) – jedna z podstawowych własności
pojęć forsingu
wprowadzona przez
izraelskiego
matematyka
Saharona Shelaha
w drugiej połowie
lat 70. XX wieku
. Nazwa jest spolszczeniem
angielskiego
wyrażenia proper forcing. W
1978
w czasie wykładów w
Berkeley
, Shelah przedstawił po raz pierwszy tę własność i jej zastosowania, w druku te idee ukazały się w
1980
[1]. W
1982
, Shelah opublikował
monografię
[2] przedstawiającą pierwsze systematyczne badania forsingów proper, związanych z nimi aksjomatów forsingowych i twierdzeń zachowawczych.[3][4][5]. DefinicjeW literaturze tematu funkcjonują trzy równoważne definicje pojęcia forsingów proper. Definicja teoriogrowa była opublikowana po raz pierwszy w rozprawie doktorskiej Charlsa Greya, pozostałe dwie są oryginalnymi definicjami Shelaha. Niech  będzie pojęciem forsingu. będzie pojęciem forsingu. Definicja kombinatoryczna- (i) Powiemy, że
zbiór
![X\subseteq [\lambda]^\omega](http://upload.wikimedia.org/math/a/0/e/a0e738963a0aa38f3851fde358085624.png) jest nieograniczony jeśli dla każdego jest nieograniczony jeśli dla każdego ![y\in [\lambda]^\omega](http://upload.wikimedia.org/math/c/2/e/c2e5faf6ad3d3d4e3f0ce5e4dd3dba40.png) możemy znaleźć możemy znaleźć  taki że taki że 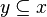 . . - (ii) Powiemy, że zbiór
![X\subseteq [\lambda]^\omega](http://upload.wikimedia.org/math/a/0/e/a0e738963a0aa38f3851fde358085624.png) jest domknięty jeśli dla każdego
ciągu jest domknięty jeśli dla każdego
ciągu
 (dla (dla  ) elementów zbioru X mamy że ) elementów zbioru X mamy że  . . - (iii) Zbiór
![S\subseteq [\lambda]^\omega](http://upload.wikimedia.org/math/4/7/2/472655534b4e578778ac40de1d1db66b.png) jest stacjonarny jeśli ma on niepusty
przekrój
z każdym domkniętym i nieograniczonym zbiorem jest stacjonarny jeśli ma on niepusty
przekrój
z każdym domkniętym i nieograniczonym zbiorem ![X\subseteq [\lambda]^\omega](http://upload.wikimedia.org/math/a/0/e/a0e738963a0aa38f3851fde358085624.png) (tzn (tzn  ). ).
- Pojęcie forsingu
 jest proper jeśli zachowuje ono stacjonarność podzbiorów jest proper jeśli zachowuje ono stacjonarność podzbiorów ![[\lambda]^\omega\](http://upload.wikimedia.org/math/9/6/2/96265232294b57093823ed53d862b897.png) dla każdej nieprzeliczalnej liczby kardynalnej λ. Innymi słowy, dla każdej nieprzeliczalnej liczby kardynalnej λ. Innymi słowy,  jest proper jeśli dla każdej nieprzeliczalnej liczby kardynalnej λ i każdego stacjonarnego zbioru jest proper jeśli dla każdej nieprzeliczalnej liczby kardynalnej λ i każdego stacjonarnego zbioru ![S\subseteq [\lambda]^\omega](http://upload.wikimedia.org/math/4/7/2/472655534b4e578778ac40de1d1db66b.png) mamy, że mamy, że  "S jest stacjonarny". "S jest stacjonarny".
Definicja teoriogrowa- Dla
 rozważmy następującą
grę nieskończoną rozważmy następującą
grę nieskończoną
 długości ω. W czasie partii tej gry, dwóch graczy (Pierwszy i Druga) konstruuje ciąg długości ω. W czasie partii tej gry, dwóch graczy (Pierwszy i Druga) konstruuje ciąg  w sposób następujący. Na kroku n, w sposób następujący. Na kroku n,
- najpierw Pierwszy wybiera
 -nazwę (term boole'owski) -nazwę (term boole'owski)  taką że taką że  " " jest
liczbą porządkową
". jest
liczbą porządkową
". - Potem Druga odpowiada wybierając liczbę porządkową
 . .
- Po skończonej partii orzekamy że Druga wygrała wtedy i tylko wtedy, gdy istnieje warunek
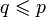 taki, że taki, że  . .
- Pojęcie forsingu
 jest proper jeśli dla każdego warunku jest proper jeśli dla każdego warunku  , Druga ma strategię zwycięską w grze , Druga ma strategię zwycięską w grze  . .
Definicja oparta na warunkach generycznych- Powiemy, że zbiór
 jest
filtrem
w jest
filtrem
w  jeśli następujące warunki są spełnione: jeśli następujące warunki są spełnione:
- (i)
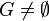 , , - (ii) jeśli
 , , 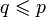 oraz oraz 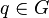 , to również , to również  , , - (iii) jeśli
 , to można znaleźć , to można znaleźć 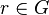 taki że taki że 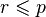 oraz oraz  . .
- Zbiór
 jest
gęstym
podzbiorem jest
gęstym
podzbiorem  jeśli jeśli  . . - Niech χ będzie
regularną
liczbą kardynalną a
 będzie rodziną wszystkich zbiorów dziedzicznie mocy mniejszej niż χ. Przypuśćmy, że N jest przeliczalnym elementarnym podmodelem będzie rodziną wszystkich zbiorów dziedzicznie mocy mniejszej niż χ. Przypuśćmy, że N jest przeliczalnym elementarnym podmodelem 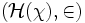 takim, że takim, że 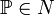 . Powiemy, że warunek . Powiemy, że warunek 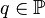 jest warunkiem jest warunkiem 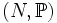 -generycznym jeśli dla każdego maksymalnego
antyłańcucha -generycznym jeśli dla każdego maksymalnego
antyłańcucha
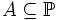 który należy do modelu N mamy który należy do modelu N mamy
dla każdego  , jeśli r,q są niesprzeczne, to , jeśli r,q są niesprzeczne, to  - (Przypomnijmy, że warunki r,q są niesprzeczne jeśli istnieje warunek
 silniejszy niż oba te warunki.) silniejszy niż oba te warunki.)
- Pojęcie forsingu
 jest proper, jeśli dla każdej dostatecznie dużej regularnej liczby kardynalnej χ istnieje jest proper, jeśli dla każdej dostatecznie dużej regularnej liczby kardynalnej χ istnieje 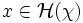 taki, że: taki, że:
- jeśli N jest przeliczalnym elementarnym podmodelem
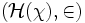 , ,  oraz oraz 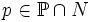 , , - to istnieje warunek
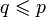 który jest który jest 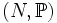 -generyczny. -generyczny.
Przykłady- Wszystkie przeliczalnie domknięte pojęcia forsingu jak też i wszystkie ccc pojęcia forsingu są proper.
- Pojęcia forsingu Lavera, Mathiasa i Sacksa (zdefiniowane w artykule o
pojęciach forsingu
) są proper.
Przykładowe własności- Przypuśćmy, że pojęcie forsingu
 jest proper. Wówczas jest proper. Wówczas
- (a) Jeśli
 oraz oraz  jest jest  -nazwą taką, że -nazwą taką, że  , to istnieją warunek , to istnieją warunek 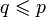 oraz ciąg oraz ciąg  zbiorów przeliczalnych takie, że zbiorów przeliczalnych takie, że  . . - (b)
 " "  jest liczbą kardynalną ". jest liczbą kardynalną ".
- Przypuśćmy, że
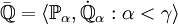 jest iteracją z nośnikami przeliczalnymi (CS iteration) taką, że dla każdego jest iteracją z nośnikami przeliczalnymi (CS iteration) taką, że dla każdego  mamy mamy
 " " 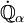 jest proper ". jest proper ".
- Wówczas
 jest proper. jest proper.
- Załóżmy
CH
. Przypuśćmy, że
 jest iteracją z nośnikami przeliczalnymi taką, że dla każdego jest iteracją z nośnikami przeliczalnymi taką, że dla każdego  mamy mamy
 " " 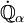 jest proper mocy co najwyżej jest proper mocy co najwyżej  ". ".
- Wówczas
 spełnia spełnia  -cc (tzn każdy antyłańcuch w -cc (tzn każdy antyłańcuch w  jest mocy co najwyżej jest mocy co najwyżej  ) oraz ) oraz  " "  " dla każdego " dla każdego  . .
Twierdzenia zachowawczePozycja własności proper w teorii forsingów iterowanych jest wynikiem szeregu twierdzeń zachowaczych związanych z tą własnością. Postać ogólnaOgólny schemat twierdzeń iteracyjnych ma następującą postać. Mamy dwie własności pojęć forsingu, powiedzmy W1 i W2 i własność W1 implikuje własność W2. Twierdzenia iteracyjne związane z tymi własnościami mogą być jednej z następujących postaci: - (a) Jeśli
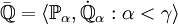 jest iteracją z nośnikami przeliczalnymi taką, że dla każdego jest iteracją z nośnikami przeliczalnymi taką, że dla każdego  mamy mamy " " 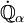 jest proper i ma własność W1 ", jest proper i ma własność W1 ",
- to
 jest proper i ma własność W2. jest proper i ma własność W2. - (b) Jeśli γ jest
liczbą graniczną
oraz
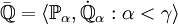 jest taką iteracją z nośnikami przeliczalnymi, że dla każdego jest taką iteracją z nośnikami przeliczalnymi, że dla każdego  mamy mamy " " 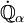 jest proper" oraz jest proper" oraz  ma własność W1, ma własność W1,
- to
 (jest proper i) ma własność W2. (jest proper i) ma własność W2.
Jeśli własności W1,W2 są identyczne, to mówimy wówczas że mamy do czynienia z twierdzeniem zachowawczym. Przykłady- Powiemy, że pojęcie forsingu
 jest ωω-ograniczające, jeśli jest ωω-ograniczające, jeśli
 . .- Twierdzenie: Jeśli
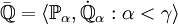 jest iteracją z nośnikami przeliczalnymi taką, że dla każdego jest iteracją z nośnikami przeliczalnymi taką, że dla każdego  mamy mamy " " 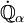 jest proper i ωω-ograniczające ", jest proper i ωω-ograniczające ",
- to
 jest proper i jest ωω-ograniczające. jest proper i jest ωω-ograniczające.
- Powiemy, że pojęcie forsingu
 jest słabo ωω-ograniczające, jeśli jest słabo ωω-ograniczające, jeśli
 jest nieskończony jest nieskończony 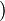 . .- Twierdzenie: Jeśli γ jest liczbą graniczną oraz
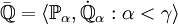 jest taką iteracją z nośnikami przeliczalnymi, że dla każdego jest taką iteracją z nośnikami przeliczalnymi, że dla każdego  mamy mamy " " 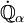 jest proper " oraz jest proper " oraz  jest słabo ωω-ograniczające, jest słabo ωω-ograniczające,
- to
 jest proper i jest słabo ωω-ograniczające. jest proper i jest słabo ωω-ograniczające.
Dalsza lekturaRozdziały 6 i 18 w monografii Shelaha[3] są najbardziej wyczerpującym przeglądem twierdzeń zachowawczych, ale bardzo jasno przedstawione szczególne przypadki tych twierdzeń można znaleźć w artykule Goldsterna[4] i książce
Tomka Bartoszyńskiego
i Haima Judaha[6]. Warto przy tej okazji zauważyć, że w artykule Goldsterna zakłada się (ze względów technicznych), że rozważane pojęcia forsingu dodają nowe liczby rzeczywiste, a prezentacja w książce Bartoszyńskiego i Judaha zawiera pewną lukę w tym aspekcie. Wyjaśnienie problemu i przedstawienie jego rozwiązania można znaleźć w artykule Jakoba Kellnera i Martina Goldsterna[7]. Aksjomat AJames E. Baumgartner[8] wprowadził własność pojęć forsingu, która implikuje, że rozważany forsing jest proper, a której sprawdzenie w wielu przypadkach jest prostsze (czy też bardziej intuicyjne). Własność ta znana jest pod nazwą aksjomatu A lub aksjomatu Baumgartnera. Aksjomat BaumgartneraPowiemy, że pojęcie forsingu  spełnia aksjomat A, jeśli istnieje ciąg
porządków częściowych spełnia aksjomat A, jeśli istnieje ciąg
porządków częściowych
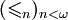 na na  taki, że taki, że - (i) jeśli
 , to , to 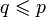 , , - (ii) jeśli
 , to , to  , , - (iii) jeśli nieskończony ciąg warunków
 ma tę własność, że ma tę własność, że 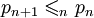 (dla wszystkich n < ω), to można znaleźć warunek (dla wszystkich n < ω), to można znaleźć warunek  taki, że taki, że  , , - (iv) dla każdego warunku
 , liczby n < ω oraz maksymalnego antyłańcucha , liczby n < ω oraz maksymalnego antyłańcucha 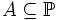 można wybrać warunek można wybrać warunek 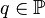 taki, że taki, że  i zbiór i zbiór 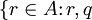 są niesprzeczne są niesprzeczne jest przeliczalny. jest przeliczalny.
Konsekwencje i przykłady- Jeśli pojęcie forsingu
 spełnia aksjomat A, to jest ono proper. spełnia aksjomat A, to jest ono proper. - Wszystkie przeliczalnie domknięte pojęcia forsingu jak też i wszystkie ccc pojęcia forsingu spełniają aksjomat A. (W pierwszym przypadku kładziemy
 , a w drugim , a w drugim  jest równością.) jest równością.) - Forsing Silvera spełnia aksjomat A. Przypomnijmy, że pojęcie forsingu Silvera
 jest zdefiniowane następująco. Elementami porządku (tzn. warunkami) są
funkcje jest zdefiniowane następująco. Elementami porządku (tzn. warunkami) są
funkcje
 takie, że takie, że  oraz oraz  jest nieskończone; porządek jest odwrotną relacją wydłużania funkcji, tzn. jest nieskończone; porządek jest odwrotną relacją wydłużania funkcji, tzn.  wtedy i tylko wtedy, gdy ( wtedy i tylko wtedy, gdy ( oraz) oraz)  . .
- Dla
liczby naturalnej
 określmy
relację
dwuczłonową określmy
relację
dwuczłonową  na na  w sposób następujący. Kładziemy w sposób następujący. Kładziemy  oraz dla n > 0: oraz dla n > 0: wtedy i tylko wtedy, gdy ( wtedy i tylko wtedy, gdy ( oraz) oraz)  i jeśli i jeśli  i i  to to  . .
- Łatwo można sprawdzić, że
 są porządkami częściowymi na są porządkami częściowymi na  zaświadczającymi, że zaświadczającymi, że  spełnia aksjomat A. spełnia aksjomat A.
- Ogólniej, pojęcia forsingu zbudowane zgodnie z metodą norm na możliwościach spełniają aksjomat A przy naturalnych warunkach[9].
Bibliografia- ↑ Shelah, Saharon: Independence results. "J. Symbolic Logic" 45 (1980), s. 563-573.
- ↑ Shelah, Saharon: Proper forcing. "Lecture Notes in Mathematics", 940. Springer-Verlag, Berlin-New York, 1982. .
- ↑ 3,0 3,1 Shelah, Saharon: Proper and improper forcing. "Perspectives in Mathematical Logic". Springer-Verlag, Berlin, 1998. .
- ↑ 4,0 4,1 Goldstern, Martin: Tools for your forcing construction. Set theory of the reals (Ramat Gan, 1991). "Israel Math. Conf. Proc.", 6, Bar-Ilan Univ., Ramat Gan, 1993, s. 305-360.
- ↑ Abraham, Uri: Proper forcing. w: Handbook of Set Theory pod red. M. Foremana, A. Kanamoriego i M. Magidora, w druku. Dostępne w formacie
dvi
na
stronie autora
.
- ↑ Bartoszyński, Tomek; Judah, Haim. Set theory. On the structure of the real line. A K Peters, Ltd., Wellesley, MA, 1995.
- ↑ Goldstern, Martin; Kellner, Jakob: New reals: can live with them, can live without them. "Math. Log. Q." 52 (2006), s. 115-124.
- ↑ Baumgartner, James E.: Iterated forcing, w: Surveys in set theory, pod red. A. R. D. Mathiasa. London Math. Soc. Lecture Notes Ser., 87, Cambridge Univ. Press, Cambridge, 1983, s. 1-59.
- ↑ Rosłanowski, Andrzej; Shelah, Saharon: Norms on possibilities. I. Forcing with trees and creatures. "Mem. Amer. Math. Soc." 141 (1999), no. 671, .
Zobacz też
Inne hasła zawierające informacje o "Proper forsing":
PFA (aksjomat)
of set-theoretic topology, s. 913-959. North-Holland, Amsterdam, 1984. Zobacz też,
hipoteza continuum
,
aksjomat Martina
,
forsing
,
pojęcie forsingu
,
Proper forsing
duże liczby kardynalne
, ...
Aksjomat Martina
in Mathematics", 940. Springer-Verlag, Berlin-New York, 1982. Zobacz też,
teoria mnogości
,
aksjomaty Zermelo-Fraenkela
,
lemat Booth'a
forsing
,
Proper forsing
,
PFA
,
CH
. ...
Tomek Bartoszyński
...
Hipoteza Kurepy
...
Pojęcie forsingu
Conf. Proc.", 6, Bar-Ilan Univ., Ramat Gan, 1993, s. 305-360. Zobacz też,
aksjomaty ZFC
,
forsing
,
Proper forsing
MA
,
PFA
. ...
Praporządek
...
Filtr (matematyka)
...
Indukcja pozaskończona
...
Algebra Boole'a
...
W. Hugh Woodin
...
Inne lekcje zawierające informacje o "Proper forsing":
 Hasło nie występuje w innych lekcjach! Hasło nie występuje w innych lekcjach!
|