Dwie przecinające się płaszczyzny w przestrzeni trójwymiarowej

Płaszczyzna – jedno z podstawowych pojęć pierwotnych geometrii Euklidesa i geometrii absolutnej . W niektórych innych aksjomatyzacjach geometrii, na przykład w geometrii analitycznej , płaszczyzna nie jest pojęciem pierwotnym, lecz zbiorem punktów .

Płaszczyznę można obrazować jako kartę papieru, powierzchnię stołu, czy płaskie pole, wyobrażając sobie je rozciągające się "w nieskończoność".

Własności

Podstawowe własności płaszczyzn opisują aksjomaty geometrii absolutnej, inne są twierdzeniami, czyli wnioskami z aksjomatów. Uwaga: niektóre z podanych własności zachodzą wyłącznie w przestrzeni trójwymiarowej.

• przez trzy niewspółliniowe punkty przestrzeni (tzn. nie leżące na jednej prostej) przechodzi jedna i tylko jedna płaszczyzna;
  • przez daną prostą i punkt nie leżący na niej przechodzi jedna i tylko jedna płaszczyzna;
  • przez dwie proste przecinające się w jednym punkcie przechodzi jedna i tylko jedna płaszczyzna;
• prosta przechodząca przez dwa różne punkty płaszczyzny zawiera się w tej płaszczyźnie;
• jeśli dwie płaszczyzny mają jeden punkt wspólny, to mają również drugi punkt wspólny;
• płaszczyzna jest zbiorem punktów przestrzeni jednakowo oddalonych od dwu ustalonych punktów;
• każdy punkt płaszczyzny należy do nieskończenie wielu prostych ;
• każda płaszczyzna dzieli przestrzeń na dwa obszary (których częścią wspólną jest ta właśnie płaszczyzna), takich że dowolny odcinek w przestrzeni ma wspólny punkt z daną płaszczyzną wtedy i tylko wtedy, gdy jego końce leża w różnych obszarach; obszary te nazywamy półprzestrzeniami – płaszczyzna jest brzegiem każdego z tych obszarów;
• każda prosta zawarta w płaszczyźnie dzieli ją na dwie części, takich że dowolny odcinek w tej płaszczyżnie ma wspólny punkt z daną prostą wtedy i tylko wtedy, gdy jego końce leża w różnych częściach; części te nazywane półpłaszczyznami ; dana prosta jest brzegiem każdej z dwu półpłaszczyzn;
• względem danej płaszczyzny prosta w przestrzeni znajduje się w jednej i tylko jednej z takich trzech pozycji:
  • nie ma punktów wspólnych z daną płaszczyzną – nazywamy ją wtedy równoległą do płaszczyzny;
  • ma jeden punkt wspólny;
  • jest zawarta w tej płaszczyźnie.

Płaszczyzna euklidesowa

Jeżeli do listy wyżej wymienionych własności dodamy następujący aksjomat (tzw. V pewnik Euklidesa ):

przez dowolny punkt płaszczyzny, nie należący do danej prostej leżącej na tej płaszczyźnie, można poprowadzić tylko jedną prostą do niej równoległą,

to otrzymamy pojęcie płaszczyzny euklidesowej. Z tym właśnie pojęciem zaznajamiamy się w szkole.

Opis w przestrzeni

jest modelem dla geometrii euklidesowej i poniższy opis dotyczy oczywiście płaszczyzny euklidesowej.

Równanie ogólne

W przestrzeni euklidesowej płaszczyzna jest zbiorem punktów, których współrzędne spełniają w danym kartezjańskim układzie współrzędnych równanie:

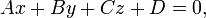
przy czym liczby 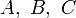nie mogą być jednocześnie równe zeru.

Jest to tak zwane równanie ogólne płaszczyzny. Wektor jest wektorem normalnym prostopadłym do tej płaszczyzny.

Równanie normalne

Równanie normalne płaszczyzny, to równanie postaci:

gdzie Liczby interpretujemy jako cosinusy kierunkowe prostej prostopadłej do płaszczyzny. Przejście z postaci ogólnej do normalnej dają wzory:

w których współczynnik normalizujący 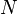odpowiada normie (długości) wektora

Równanie odcinkowe

Do opisu płaszczyzny można też użyć równania odcinkowego:

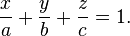
Ma ono tę zaletę, że od razu daje punkty przecięcia płaszczyzny z osiami współrzędnych układu: są to punkty

Ma również istotną wadę: nie daje się w ten sposób przedstawić żadnej płaszczyzny przechodzącej przez początek układu współrzędnych (wówczas wszystkie mianowniki musiałyby być równe zeru, 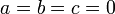) ani też żadnej płaszczyzny równoległej do którejkolwiek osi (wówczas odpowiedniemu współczynnikowi lub parze współczynników należałoby przypisać wartość nieskończoną, ).

Przejście z postaci ogólnej lub normalnej do odcinkowej dają wzory:

Płaszczyzna przechodząca przez trzy punkty

Ponieważ istnieje tylko jedna płaszczyzna w przechodząca przez trzy niewspółliniowe punkty, dlatego można jednoznacznie wyznaczyć tę płaszczyznę. Jeżeli płaszczyzna przechodzi przez trzy punkty 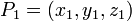, i 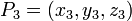, jest określona następującym równaniem:

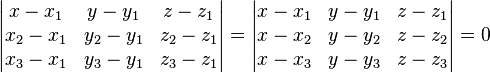
lub

Odległość punktu od płaszczyzny

Odległość punktu P o współrzędnych 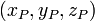od płaszczyzny m zadanej równaniem ogólnym lub normalnym przedstawia wzór:

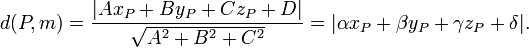
Zobacz też

• prosta
• półpłaszczyzna
• hiperpłaszczyzna