|
Obraz (matematyka)
Obraz (matematyka)Obraz –
zbiór
wszystkich wartości przyjmowanych przez
funkcję
dla każdego elementu danego
podzbioru
jej
dziedziny
. Przeciwobraz danego podzbioru
przeciwdziedziny
funkcji to zbiór wszystkich elementów dziedziny, które są odwzorowywane na elementy wspomnianego podzbioru. Obraz i przeciwobraz można zdefiniować nie tylko dla funkcji, ale ogólnie dla wszystkich relacji dwuargumentowych. DefinicjaSłowo „obraz” może oznaczać jedno z trzech poniższych, powiązanych ze sobą, pojęć. Dalej  oznacza
funkcję
zbioru X w zbiór Y. oznacza
funkcję
zbioru X w zbiór Y. - Obraz elementu
- Jeżeli x jest elementem X, to f(x) = y, czyli wartość funkcji f na elemencie x, nazywa się obrazem x poprzez f.
- Obraz zbioru
- Obrazem zbioru
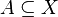 w funkcji f nazywa się podzbiór w funkcji f nazywa się podzbiór ![f[A] \subseteq Y](http://upload.wikimedia.org/math/9/d/8/9d859a82a42191b73c4c91726f99009b.png) wszystkich obrazów elementów tego zbioru, tzn. zbiór wszystkich obrazów elementów tego zbioru, tzn. zbiór
- Jeżeli nie istnieje ryzyko pomyłki f[A] oznacza się zwykle symbolem f(A). Zapis ten pozwala na interpretację obrazu poprzez f jako funkcji, której dziedziną jest
zbiór potęgowy
(wszystkie podzbiory) zbioru X, a przeciwdziedziną zbiór potęgowy zbioru Y.
- Obraz funkcji
Obraz f[X] całej dziedziny X nazywa się zwykle obrazem funkcji f. Do innych oznaczeń należą również f(X) (j.w.),  (ang. image – obraz). (ang. image – obraz). PrzeciwobrazNiech f oznacza funkcję zbioru X w zbiór Y. Przeciwobrazem zbioru 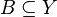 względem f nazywa się podzbiór zbioru X określony wzorem względem f nazywa się podzbiór zbioru X określony wzorem ![f^{-1}[B] = \{x \in X\colon f(x) \in B\}.](http://upload.wikimedia.org/math/7/3/5/735b67fdb8923e87b3161343225fd088.png)
Przeciwobraz zbioru jednoelementowego, oznaczany symbolem ![f^{-1}[\scriptstyle\{y\}\textstyle]](http://upload.wikimedia.org/math/b/1/d/b1db003d6e9d1afbeb58a7a4897277fa.png) lub krótko f − 1[y] nazywa się również włóknem nad y bądź
poziomicą
lub warstwicą y. Zbiór wszystkich włókien nad elementami Y tworzy
rodzinę zbiorów indeksowaną
przez Y. Prowadzi to do pojęcia kategorii rozwłóknień. lub krótko f − 1[y] nazywa się również włóknem nad y bądź
poziomicą
lub warstwicą y. Zbiór wszystkich włókien nad elementami Y tworzy
rodzinę zbiorów indeksowaną
przez Y. Prowadzi to do pojęcia kategorii rozwłóknień. Raz jeszcze, jeśli nie ma ryzyka pomyłki, to f − 1[B] można oznaczać symbolem f − 1(B) i myśleć o f − 1 jako o funkcji ze zbioru potęgowego Y w zbiór potęgowy X. Oznaczenie f − 1 może przywodzić na myśl notację odrębnego pojęcia
funkcji odwrotnej
, które pokrywa się z pojęciem przeciwobrazu wtedy i tylko wtedy, gdy f jest
bijekcją
. NotacjaTradycyjne sposoby zapisu przedstawione w wyżej mogą prowadzić do nieścisłości. Alternatywą[1] może być wyodrębnienie oddzielnych nazw dla obrazu i przeciwobrazu jako funkcji między zbiorami potęgowymi: - Notacja strzałkowa
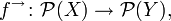 gdzie gdzie   gdzie gdzie 
- Notacja gwiazdkowa
 zamiast zamiast   zamiast zamiast 
- Inne
- Alternatywną notacją f[A] wykorzystywaną m.in. w
logice matematycznej
i
teorii mnogości
jest f''A.
- W niektórych pracach obraz f nazywa się także „zbiorem wartości”, jednak w ogólności powinno unikać się tego wyrażenia, ponieważ niekiedy terminem tym określa się jednak całą przeciwdziedzinę. Podobny problem istnieje w języku angielskim, z którego zapożyczono oznaczenia obrazu funkcji f postaci
 bądź bądź  (ang. range – zbiór wartości, przeciwdziedzina; dosł. zakres). (ang. range – zbiór wartości, przeciwdziedzina; dosł. zakres).
Przykłady określona wzorem określona wzorem  - Obrazem zbioru {2,3} poprzez f jest
![f[\scriptstyle\{2, 3\}\textstyle] = \{a, c\}.](http://upload.wikimedia.org/math/9/2/3/923600861cfa89bb8c6b02e564a98c06.png) Obrazem funkcji jest {a,c}. Przeciwobrazem a jest f − 1[a] = {1,2}. Przeciwobrazem {a,b} również jest {1,2}. Przeciwobrazem {b,d} jest
zbiór pusty
{}. Obrazem funkcji jest {a,c}. Przeciwobrazem a jest f − 1[a] = {1,2}. Przeciwobrazem {a,b} również jest {1,2}. Przeciwobrazem {b,d} jest
zbiór pusty
{}.
 dana wzorem f(x) = x2. dana wzorem f(x) = x2.- Obrazem { − 2,3} w f jest
![f[\scriptstyle\{2, 3\}\textstyle] = \{4, 9\},](http://upload.wikimedia.org/math/f/0/a/f0ac21d66a94b9505caa005d7d6e9442.png) a obrazem f jest a obrazem f jest 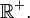 Przeciwobraz {4,9} w f to Przeciwobraz {4,9} w f to ![f^{-1}[\scriptstyle\{4, 9\}\textstyle] = \{-3, -2, 2, 3\}.](http://upload.wikimedia.org/math/2/9/d/29d45f3fdca284fcaa51d888aac7d4e6.png) Przeciwobrazem zbioru Przeciwobrazem zbioru  w f jest zbiorem pustym, ponieważ liczby ujemne nie mają
pierwiastków kwadratowych
w zbiorze
liczb rzeczywistych
. w f jest zbiorem pustym, ponieważ liczby ujemne nie mają
pierwiastków kwadratowych
w zbiorze
liczb rzeczywistych
.
 dana wzorem f(x,y) = x2 + y2. dana wzorem f(x,y) = x2 + y2.- Włóknami (poziomicami) f − 1[a] są
okręgi
o wspólnym środku w
początku
układu współrzędnych
, sam początek i
zbiór pusty
, w zależności od wartości parametru a, odpowiednio: a > 0, a = 0 oraz a < 0.
- Jeżeli M jest
rozmaitością
, a
 jest
rzutem
kanonicznym
wiązki stycznej jest
rzutem
kanonicznym
wiązki stycznej
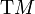 na M, to
przestrzenie styczne na M, to
przestrzenie styczne
 dla dla  Jest to przykład wiązki włóknistej. Jest to przykład wiązki włóknistej.
WłasnościNiech dana będzie funkcja  Dla wszystkich podzbiorów Dla wszystkich podzbiorów  oraz oraz  zachodzą następujące własności: zachodzą następujące własności: - obraz jest podzbiorem przeciwdziedziny, a przeciwobraz – dziedziny,
![f[A] \subseteq Y](http://upload.wikimedia.org/math/9/d/8/9d859a82a42191b73c4c91726f99009b.png) oraz oraz ![f^{-1}[B] \subseteq X;](http://upload.wikimedia.org/math/2/d/9/2d9f9767abc37eced21c40d0c61d8ea0.png)
- działania brania obrazu i przeciwobrazu związane są ze sobą następującymi relacjami:
![f[\scriptstyle f^{-1}[B]\textstyle] \subseteq B](http://upload.wikimedia.org/math/f/7/b/f7bdc0fb399b2982a5493d15a3f94c19.png) (równość dla
funkcji „na”
), (równość dla
funkcji „na”
),![f^{-1}[\scriptstyle f[A]\textstyle] \supseteq A](http://upload.wikimedia.org/math/2/f/e/2feb9d32697b317bcefc025eb1e1aeac.png) (równość dla
funkcji różnowartościowej
), (równość dla
funkcji różnowartościowej
),![f[A] \subseteq B \Leftrightarrow A \subseteq f^{-1}[B];](http://upload.wikimedia.org/math/8/0/0/80066dfd25506f04c674c4151acd27ad.png)
- operacje obrazu i przeciwobrazu są
monotoniczne
, tzn.
![A_1 \subseteq A_2 \Rightarrow f\left[A_1\right] \subseteq f\left[A_2\right]](http://upload.wikimedia.org/math/7/2/5/725c350fe330c3b2bbaca6af718b5a0f.png) oraz oraz![B_1 \subseteq B_2 \Rightarrow f^{-1}\left[B_1\right] \subseteq f^{-1}\left[B_2\right];](http://upload.wikimedia.org/math/e/e/4/ee4ed1820ded9e89b482e26e25473e3d.png)
- prawdziwe są także poniższe związki z działaniami brania
sumy
i
przekroju
zbiorów:
![f[A \cup B] = f[A] \cup f[B],](http://upload.wikimedia.org/math/1/0/9/109e560c78ae7ce7ef653fd7d42bc4e6.png) ![f[A \cap B] \subseteq f[A] \cap f[B]](http://upload.wikimedia.org/math/e/7/b/e7b7939e0b2d5beea453a55154257035.png) (równość, gdy funkcja jest różnowartościowa), (równość, gdy funkcja jest różnowartościowa),![f^{-1}[A \cup B] = f^{-1}[A] \cup f^{-1}[B],](http://upload.wikimedia.org/math/b/a/8/ba84aa91e095657242cbf56581c865bc.png) ![f^{-1}[A \cap B] = f^{-1}[A] \cap f^{-1}[B];](http://upload.wikimedia.org/math/2/1/b/21b51910db681929eac3fe6af0a9f321.png)
- zachodzi również następujący związek z braniem
dopełnienia
zbioru:
![f^{-1}\left[B^{\operatorname c}\right] = (f^{-1}[B])^{\operatorname c},](http://upload.wikimedia.org/math/e/9/6/e9646837648e2945b80419c5ab343d2b.png)
- z powyższych wynikają w szczególności te oto relacje z
różnicą zbiorów
:
![f\left[A \setminus B\right] \supseteq f[A] \setminus f[B],](http://upload.wikimedia.org/math/1/f/1/1f1c118faa2a3a0add2c974a10e6d685.png) ![f^{-1}\left[A \setminus B\right] = f^{-1}[A] \setminus f^{-1}[B]](http://upload.wikimedia.org/math/4/a/7/4a76175c9ee1bacb1a8115817723cc06.png) . .
- istnieje też tożsamość wiążąca przeciwobraz z
zawężeniem
funkcji:
![(f|_A)^{-1}[B] = A \cap f^{-1}[B].](http://upload.wikimedia.org/math/c/b/e/cbe2a61e9fea5d8028c9cd850f3b4ced.png)
Wyżej przedstawione stosunki łączące obrazy i przeciwobrazy z algebrą (
Boole'a
) przekrojów i sum zachodzą nie tylko dla par zbiorów (a przez
indukcję
– skończonej ich liczby), ale także dla dowolnej rodziny podzbiorów (także nieprzeliczalnej). Niech  będzie
rodziną indeksowaną
podzbiorów X, a będzie
rodziną indeksowaną
podzbiorów X, a  będzie rodziną indeksowaną podzbiorów Y. Wówczas będzie rodziną indeksowaną podzbiorów Y. Wówczas oraz W języku algebry podzbiorów powyższe obserwacje oznaczają, że funkcja brania przeciwobrazu jest
homomorfizmem krat
, zaś funkcja obrazu jest tylko
homomorfizmem półkrat
(ponieważ nie zawsze zachowuje przekroje). Przeciwobraz zbioru  względem
złożenia względem
złożenia
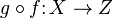 dwóch funkcji dwóch funkcji  oraz oraz  dany jest wzorem: dany jest wzorem: Zobacz też LiteraturaPrzypisy
Inne hasła zawierające informacje o "Obraz (matematyka)":
Wszystkich Świętych
...
Iloczyn
...
Nadciśnienie tętnicze
...
Adwentyzm
...
Uniwersytet Witolda Wielkiego
...
Widmo
...
Wskaźnik
...
Grupa
...
John William Waterhouse
...
Wojciech Brudzewski
...
Inne lekcje zawierające informacje o "Obraz (matematyka)":
Potęgi (plansza 2)
...
Pierwiastki (plansza 1)
...
Rozwinięcia dziesiętne (plansza 1)
...
|