W topologii zbiór nazywamy zbiorem pierwszej kategorii jeżeli można go przedstawić w postaci przeliczalnej sumy zbiorów nigdziegęstych .

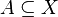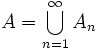Bardziej formalnie, niech (X,τ) będzie przestrzenią topologiczną . Powiemy że zbiór jest pierwszej kategorii Baire'a w X (lub I kategorii) jeśli można go przedstawić jako sumę , gdzie każdy ze zbiorów A_n jest nigdziegęsty w X (tzn ). Rodzinę wszystkich zbiorów pierwszej kategorii w X będziemy oznaczać przez (albo po prostu przez 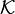jeśli jest jasne o jakiej przestrzeni topologicznej mówimy).

Zbiory które nie są pierwszej kategorii nazywane są zbiorami drugiej kategorii Baire'a (lub II kategorii).

Własności

• Zbiory pierwszej kategorii w przestrzeni X tworzą σ-ideał podzbiorów X. Każdy zbiór z jest zawarty w pewnym zbiorze typu Fσ który też jest pierwszej kategorii.
• Otwarte niepuste podzbiory przestrzeni zupełnej nie są pierwszej kategorii w tej przestrzeni.
• Doskonałe przestrzenie polskie wyglądają tak samo jeśli patrzymy na ich podzbiory borelowskie i zbiory pierwszej kategorii: jeśli X,Y są doskonałymi przestrzeniami polskimi to istnieje izomorfizm borelowski 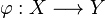który zachowuje zbiory pierwszej kategorii (tzn wtedy i tylko wtedy gdy ).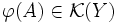
• Każda rodzina rozłącznych borelowskich podzbiorów prostej rzeczywistej 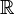które nie są pierwszej kategorii jest co najwyżej przeliczalna.

Przykłady i zastosowanie

• Każdy przeliczalny podzbiór prostej rzeczywistej jest I kategorii w . W szczególności zbiór liczb wymiernych jest pierwszej kategorii (choć jest to gęsty podzbiór ).
• Prostą rzeczywistą można przedstawić jako sumę dwóch zbiorów, , takich że

K jest zbiorem pierwszej kategorii, a

L jest zbiorem miary zero Lebesgue'a .

Aby podać przykład takich zbiorów K,L ustalmy numerację zbioru liczb wymiernych. (Przypomnijmy, że zbiór liczb wymiernych jest przeliczalny .) Dla liczb naturalnych n,m niech będzie odcinkiem otwartym o środku w q_n i długości 2 ^{− (n + m)}. Wówczas zbiór 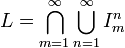jest miary zero, ale jego dopełnienie 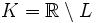jest pierwszej kategorii.

• Inny przykład rozkładu jak powyżej jest dany przez liczby Liouville'a : zbiór liczb Liouville'a jest miary zero na prostej, a jego dopełnienie jest zbiorem pierwszej kategorii.
• Polski matematyk Stefan Banach przedstawił w 1931 następujące spektakularne zastosowanie zbiorów pierwszej kategorii. Niech będzie przestrzenią wszystkich funkcji ciągłych z odcinka [0,1] w zbiór liczb rzeczywistych . Wyposażmy w topologię zbieżności jednostajnej zadanej przez metrykę

Wówczas jest przestrzenią polską. Rozważmy zbiór

nie ma pochodnej w żadnym punkcie odcinka

Banach udowodnił, że zbiór jest pierwszej kategorii w , czyli że z topologicznego punktu widzenia prawie każda funkcja ciągła nie jest różniczkowalna w żadnym punkcie.

Gra Banacha-Mazura

Ze zbiorami pierwszej kategorii związana jest (najprawdopodobniej) pierwsza z pozycyjnych gier nieskończonych rozważanych w matematyce. Gra ta była opisana przez polskiego matematyka Stanisława Mazura w Problemie 43 w Księdze Szkockiej . Odpowiedź na pytanie Mazura była dana przez Stefana Banacha w 1935 .

Niech Z będzie dowolnym podzbiorem . Rozważmy następującą grę dwóch graczy, oznaczanych przez A i B. Gracze wykonuja nieskończenie wiele posunięć ponumerowanych liczbami naturalnymi . Zaczynają w ten sposób, że Gracz A wybiera niepusty przedział otwarty I₁ a Gracz B odpowiada przez wskazanie niepustego otwartego przedziału . Kiedy gracze dochodzą do ntego kroku w grze, to mają oni skontruowany zstępujący ciąg niepustych przedziałów otwartych 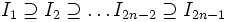. Na ntym etapie gry najpierw Gracz A wybiera niepusty przedział otwarty 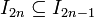, a potem Gracz B wskazuje niepusty otwarty przedział .

Kiedy gracze wykonają już wszystkie posunięcia (jest ich nieskończenie wiele!), to decydujemy że Gracz B wygrał partię wtedy i tylko wtedy gdy .

Okazuje się, że Gracz B ma strategię zwycięską w tej grze wtedy i tylko wtedy gdy zbiór jest pierwszej kategorii.

Zobacz też

• ,
• zbiór nigdziegęsty ,
• diagram Cichonia ,
• własność Baire'a ,
• ideały w teorii mnogości .