Ideał – w teorii porządków częściowych , teorii mnogości i pokrewnych dziedzinach matematyki pojęcie dualne do pojęcia filtru .

Intuicje

Najogólniejsza definicja ideału jest formułowana dla częściowych porządków, ale jej specjalny przypadek ideału podzbiorów danego zbioru jest najlepszym źródłem intuicji. W tym ograniczonym kontekście, ideał to rodzina zbiorów w jakimś sensie małych. Wydaje się naturalnym, że pojęcie małych zbiorów powinno spełniać pewne podstawowe własności:

• zbiór mniejszy od małego zbioru powinien być mały,
• zbiór pusty powinien być mały, ale cała przestrzeń ( uniwersum ) nie powinna być mała,
• suma dwóch małych zbiorów powinna być mała.

Rodzina zbiorów spełniająca powyższe wymagania (jako rodzina zbiorów małych) jest właśnie ideałem zbiorów, patrz poniżej.

Definicje

Ideały w porządkach

Niech 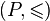będzie porządkiem częściowym. Powiemy, że zbiór jest ideałem w zbiorze uporządkowanym P jeśli następujące warunki są spełnione:

(i) ,

(ii) jeśli , 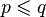oraz , to również ,

(iii) jeśli 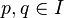, to można znaleźć taki że oraz .

Ideał I jest właściwy jeśli dodatkowo

(iv) .

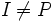Ideały w algebrach Boole'a

Ponieważ algebra Boole'a jest także zbiorem częściowo uporządkowanym, to definicja ideału w porządkach częściowych może być przeniesiona bez zmian na algebry Boole'a. Możemy jednak wykorzystać fakt, że porządek boole'owski jest związany z operacjami algebry i możemy sformułować definicję ideału trochę inaczej.

Niech 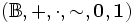będzie algebrą Boole'a. Powiemy, że zbiór I jest ideałem w algebrze Boole'a 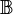jeśli następujące warunki są spełnione:

(i) ,

(ii) jeśli , 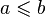(tzn ) oraz , to również ,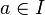

(iii) jeśli , to .

Ideał I jest właściwy jeśli dodatkowo

(iv) .

Należy podkreślić, że powyższa definicja i ta przeniesiona z porządków częściowych są równoważne.

Ideały podzbiorów danego zbioru

Szczególnym przypadkiem algebry Boole'a jest rodzina wszystkich podzbiorów ustalonego zbioru S (z operacjami sumy, przekroju i dopełnienia zbiorów). Zatem sformułowana powyżej definicja ideału na algebrze Boole'a może być powtórzona bez zmian dla podzbiorów zbioru S. Sformułujemy tę definicję jeszcze raz dla podkreślenia znaczenia intuicji, że ideał to rodzina małych podzbiorów S.

Niech S będzie niepustym zbiorem. Powiemy, że rodzina I podzbiorów zbioru S jest ideałem podzbiorów zbioru S jeśli następujące warunki są spełnione:

(i) ,

(ii) jeśl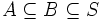i i , to również ,

(iii) jeśli 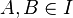, to .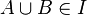

Ideał I jest właściwy jeśli dodatkowo

(iv) .

Ideały maksymalne

Ideał właściwy I w porządku częściowym 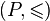jest ideałem maksymalnym jeśli jedynym ideałem właściwym zawierającym I jest samo I.

Przykłady

Ideały w algebrach Boole'a

• Niech 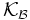będzie rodziną tych borelowskich podzbiorów prostej rzeczywistej które są pierwszej kategorii . Wówczas 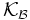jest ideałem w algebrze borelowskich podzbiorów prostej.
• Niech będzie rodziną tych borelowskich podzbiorów prostej, które są miary zero Lebesgue'a . Wówczas jest ideałem w algebrze borelowskich podzbiorów prostej.
• Przypuśćmy, że F jest filtem w algebrze Boole'a 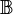. Niech . Wówczas F^c jest ideałem w 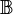. Warto zauważyć, że F^c jest ideałem maksymalnym wtedy i tylko wtedy gdy F jest ulltrafiltrem.

Ideały podzbiorów danego zbioru

• Niech S będzie zbiorem nieskończonym. Rodzina [S] ^{< ω} wszystkich skończonych podzbiorów S jest ideałem podzbiorów S. Jest on często nazywany ideałem Frécheta .
• Niech . Wówczas rodzina I_A wszystkich podzbiorów zbioru A jest ideałem podzbiorów X. Ideały tej postaci są nazywane ideałami głównymi i zwykle nie są one obiektem rozważań (tzn typowym założeniem o rozważanych ideałach jest że są one niegłówne).
• Niech 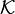będzie rodziną wszystkich podzbiorów prostej rzeczywistej które są pierwszej kategorii, a 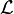będzie rodziną tych wszystkich podzbiorów prostej które mają miarę Lebesgue'a zero. Wówczas zarówno 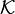jak i 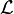są ideałami podzbiorów prostej.
• Przypuśćmy, że (X,τ) jest przestrzenią topologiczną . Wówczas rodzina wszystkich nigdziegęstych podzbiorów przestrzeni X tworzy właściwy ideał podzbiorów X.
• Niech κ będzie nieprzeliczalną regularną liczbą kardynalną . Rozważmy rodzinę tych podzbiorów κ których dopełnienie zawiera domknięty nieograniczony podzbiór κ. jest ideałem podzbiorów κ - zbiory z tego ideału są nazywane niestacjonarnymi podzbiorami κ.

Dodatkowe pojęcia

• Niech κ będzie nieskończoną liczbą kardynalną. Mówimy, że ideał I podzbiorów zbioru S jest κ-zupełny, jeśli suma mniej niż κ zbiorów z ideału I należy do I.
• Ideały -zupełne na S są nazywane σ-ideałami podzbiorów S. Tak więc σ-ideał podzbiorów S, to taki ideał I podzbiorów S, który spełnia następujący warunek:

(iii)^σ jeśli , to .

• Czasami dla ideałów podzbiorów jakiegoś zbioru bada się następujące funkcje kardynalne , nazywane też współczynnikami kardynalnymi ideału. Niech I będzie takim ideałem podzbiorów zbioru S, który zawiera wszystkie zbiory jednopunktowe. Określamy:

Własności i i zastosowania

• Każdy właściwy ideał w algebrze Boole'a jest zawarty w pewnym ideale maksymalnym. (To twierdzenie, udowodnione przez Tarskiego , wymaga pewnej formy AC .)
• Jeśli I jest ideałem podzbiorów S który zawiera wszystkie zbiory jednopunktowe, to

i .

• Wspólczynniki kardynalne ideałów i były intensywnie studiowane także i w Polsce w latach 80. XX wieku . Są one głównymi elementami tzw. diagramu Cichonia .

Zobacz też

• Filtr
• Diagram Cichonia