Przestrzeń mierzalna i σ-ciało zbiorów – obiekty studiowane w matematyce , przede wszystkim w teorii mnogości , teorii miary i rachunku prawdopodobieństwa (w ostatnich dwóch dziedzinach w powiązaniu z miarami ).

Wprowadzenie

Już we wczesnych latach rozwoju teorii miary i teorii mnogości zauważono, że przy założeniu aksjomatu wyboru istnieją zbiory na prostej rzeczywistej , dla których nie można określić miary Lebesgue'a ; przykładem takiego zbioru jest zbiór Vitalego . Później odkryto, że odrzucenie aksjomatu wyboru, a przyjęcie aksjomatu determinacji gwarantuje mierzalność wszystkich podzbiorów (twierdzenie Jana Mycielskiego i Stanisława Świerczkowskiego^[1]). Stwierdzono również, że odpowiednie aksjomaty dużych liczb kardynalnych mogą dostarczyć sposobów mierzenia wszystkich podzbiorów prostej rzeczywistej.

Z różnych powodów tego typu dodatkowe założenia mogą być nie pożądane, wówczas należy uznać, że mogą istnieć zbiory tak dziwne, że określenie ich wielkości (tzn. miary ) nie jest możliwe. Na ogół takie zbiory nie pojawiają się „nieproszone” i w praktyce matematycznej wystarczające okazuje się ograniczenie do dobrych zbiorów, które powinny być zamknięte na jak najszerszą klasę podstawowych operacji. Za takie uważa się przekrój , sumę , czy też dopełnienie (z tego też powodu w teorii miary większy nacisk kładzie się na operację brania przeciwobrazu , który zachowuje te operacje w przeciwieństwie do operacji brania obrazu ; zob. funkcja mierzalna ). Z tego powodu zbiór skonstruowany z dobrych zbiorów za pomocą wspomnianych operacji również powinien być dobry. Zaakceptowanie poprzedniego stwierdzenia oznacza (na podstawie zasady indukcji ) przyzwolenie na konstruowanie dobrych zbiorów ze skończonej liczby zbiorów połączonych wspomnianymi trzema działaniami. Rodziny tego rodzaju były badane, lecz rezultaty okazały się mało istotne. Dopiero rozszerzenie definicji poprzez zezwolenie na działania nieskończone, ale przeliczalne , doprowadziło do rozkwitu wspomnianych wyżej dziedzin. Pojęcie σ-ciała może być uznane za abstrakcyjną definicję opisanej wyżej rodziny dobrych zbiorów.

Definicje

Dla ustalonej przestrzeni X σ-ciałem jej zbiorów nazywa się przeliczalnie addytywne ciało podzbiorów zbioru X. Dokładniej, rodzina podzbiorów niepustego zbioru X stanowi σ-ciało, jeśli

• zbiór pusty należy do

  

• dopełnienie zbioru należącego do należy do

  

• suma przeliczalnie wielu zbiorów należących do należy do

  

σ-ciała zbiorów są też czasami nazywane σ-algebrami zbiorów.

Przestrzenią mierzalną nazywa się parę uporządkowaną gdzie oznacza pewne σ-ciało podzbiorów przestrzeni X. Przestrzeń (mierzalna) z miarą to trójka uporządkowana , gdzie 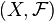jest przestrzenią mierzalną, a

jest ( σ-addytywną ) miarą . Przestrzeń (mierzalną) z miarą probabilistyczną określa się również nazwą „ przestrzeń probabilistyczna ”.

Własności

Ponieważ każde σ-ciało jest zamknięte na przekroje przeliczalne, to przekrój dowolnej rodziny σ-ciał na X jest znów σ-ciałem zbiorów. Dowodzi się, że dla dowolnej rodziny 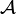podzbiorów zbioru X istnieje najmniejsze σ-ciało zbiorów zawierające wszystkie zbiory tej rodziny. Nazywa się je σ-ciałem generowanym przez tę rodzinę i oznacza symbolem bądź . Niech będzie σ-ciałem podzbiorów X, a będzie σ- ideałem podzbiorów X. Wówczas σ-ciałem generowanym przez 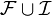jest zbiór

gdzie oznacza operację różnicy symetrycznej .

Przykłady

Niech X będzie niepustym zbiorem. Wówczas następujące rodziny podzbiorów X są σ-ciałami na X:

• rodzina złożona ze zbioru pustego i zbioru X – jest to najmniejsze σ-ciało określone na X,
• rodzina wszystkich podzbiorów zbioru X – jest to z kolei największe σ-ciało na danym zbiorze,
• rodzina dla dowolnego
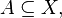
• każde skończone ciało podzbiorów X.

Niech (X,τ) będzie przestrzenią topologiczną . Wówczas elementy σ-ciała σ(τ) nazywa się zbiorami borelowskimi przestrzeni X.

• Niech będzie σ-ciałem podzbiorów borelowskich prostej rzeczywistej a oznacza σ-ideał zbiorów miary zero (w sensie Lebesgue'a), zaś będzie σ-ideałem zbiorów pierwszej kategorii (w sensie Baire'a). Wówczas

jest zbiorem typu G_δ} jest mierzalnych w sensie Lebesgue'a

oraz

jest zbiorem otwartym} jest o własności Baire'a .

Jeśli λ jest miarą Lebesgue'a na prostej, to jest przestrzenią z miarą.

Zobacz też

• funkcja mierzalna
• algebra Boole'a
• klasa monotoniczna
• zbiór borelowski

Przypisy