Kwaterniony – struktura algebraiczna ( liczby ) będąca rozszerzeniem ciała liczb zespolonych . Kwaterniony zostały wprowadzone przez irlandzkiego matematyka Williama Hamiltona w 1843 i służyły opisowi mechaniki w przestrzeni trójwymiarowej. Początkowo kwaterniony były uważane za twór patologiczny, ponieważ nie spełniały reguły przemienności (należy mieć na uwadze, iż kwaterniony pojawiły się przed macierzami). Kwaterniony znajdują zastosowanie tak w matematyce teoretycznej jak i stosowanej, zobacz sekcję Zastosowania.

Współczesna matematyka opisuje kwaterniony jako czterowymiarową, unormowaną algebrę z dzieleniem nad liczbami rzeczywistymi . Algebra kwaternionów jest oznaczana przez 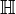od pierwszej litery nazwiska twórcy. Wspomniana algebra 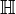zajmuje specjalne miejsce w algebrze , ponieważ zgodnie z twierdzeniem Frobeniusa jest jednym z trzech skończenie wymiarowych pierścieni z dzieleniem zawierających liczby rzeczywiste jako podpierścień .

Zapis

Jest kilka sposobów przedstawiania kwaternionów. Jednym z nich jest przedstawienie kwaternionów w postaci macierzowej, czyli jako macierzy z przestrzeni takich, że

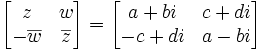, gdzie .

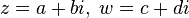Innym sposobem zapisu macierzowego jest^[1]

, dla .

Kolejnym sposobem zapisu jest postać algebraiczna – wprowadzenie oznaczenia dla szczególnych macierzy (kwaternionów)

pozwoli na zapis dowolnego kwaternionu w postaci

q = a + bi + cj + dk, gdzie .

Wtedy nazywa się czasami częścią rzeczywistą kwaternionu q.

Dodatkowo niech dla .

Sprzężenie, wyznacznik, moduł

Sprzężenie w kwaternionach definiujemy następującym wzorem:

,

w postaci algebraicznej:

.

Wyznacznik kwaternionu definiujemy wg wzoru

detq = | z | ² + | w | ².

Moduł to pierwiastek z wyznacznika:

,

albo równoważnie w postaci algebraicznej:

Własności sprzężenia i modułu

• ,
• ,
• ,
• ( nierówność trójkąta ).

Własności

Wykorzystując wspomniany izomorfizm kwaternionów i ich postaci macierzowej otrzymujemy:

• z własności dodawania macierzy wnioskujemy, iż suma dwu kwaternionów jest kwaternionem;

• podobnie iloczyn dwu kwaternionów jest kwaternionem,
• dla kwaternionu :
  • ,
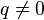  • istnieje kwaternion odwrotny zadany wzorem

.

Zauważmy jeszcze iż:

• mnożenie kwaternionów jest łączne, czyli (ab)c = a(bc),
• zachodzą rozdzielności mnożenia względem dodawania, czyli
  • x(y + z) = xy + xz,
  • (y + z)x = yx + zx.

Tak zdefiniowane kwaterniony i,j,k spełniają następujące zależności:

• i² = j² = k² = ijk = − 1,
• ij = − ji = k,
• jk = − kj = i,
• ki = − ik = j,
• 1q = q1 = q dla dowolnego q, czyli 1 jest elementem neutralnym mnożenia,
• rq = qr o ile (jest kwaternionem postaci r + 0i + 0j + 0k), natomiast q dowolnym kwaternionem.
• .

Izomorficzność

Ponieważ kwaterniony są uogólnieniem pewnych ciał liczbowych, poniżej wskazujemy izomorfizmy pewnych podzbiorów kwaternionów z tymi ciałami:

• kwaterniony postaci można utożsamiać z liczbami rzeczywstymi,
• następujące zbiory kwaternionów możemy utożsamiać z ciałem liczb zespolonych :
  • ,
  • ,
  • .

Własności algebraiczne

Grupa kwaternionów

Z powyższych własności i praw działań na macierzach wnioskujemy, iż zbiór {1, − 1,i, − i,j, − j,k, − k} z mnożeniem tworzy grupę oznaczaną symbolem Q₈ (od liczby elementów).

Zbiór kwaternionów z dodawaniem jako działaniem tworzy grupę abelową (zbiór z mnożeniem nie jest grupą abelową), a ponieważ działanie mnożenia jest łączne i zachodzi jego rozdzielność obustronna względem dodawania, to kwaterniony ze wspomnianymi dwoma działaniami tworzą pierścień nieprzemienny (ponieważ ), w którym rozwiązywalne są równania postaci Ax + B = C oraz .

Pierścień z dzieleniem

Co więcej: zbiór kwaternionów z działaniami dodawania i mnożenia tworzy pierścień z dzieleniem , spełnione są w nim wszystkie aksjomaty ciała z wyjątkiem warunku ab = ba.

Przykłady

Niech

x = 2 + 3i + 4k

y = 2 + 3j + 2k

Wtedy

x + y = 4 + 3i + 3j + 6k,

xy = (2 + 3i + 4k)(2 + 3j + 2k) =

= 2(2 + 3j + 2k) + 3i(2 + 3j + 2k) + 4k(2 + 3j + 2k) =

= 4 + 6j + 4k + 6i + 9ij + 6ik + 8k + 12kj + 8k² =

= 4 + 6j + 4k + 6i + 9k + 6( − j) + 8k + 12( − i) + 8( − 1) =

= − 4 − 6i + 21k

Geometryczna interpretacja mnożenia

Jak liczbę zespoloną tak i kwaternion można przedstawić w postaci sumy części rzeczywistej oraz urojonej a + v. W tej postaci , zaś wektorem trójwymiarowym. Wtedy iloczyn dwóch wektorów urojonych można wyrazić jako: , a dwóch kwaternionów - jako: . We wzorach tych kropka oznacza iloczyn skalarny , a krzyżyk iloczyn wektorowy w przestrzeni trójwymiarowej.

Obroty przestrzeni trójwymiarowej

Kwaterniony jednostkowe tworzą sferę jednostkową S³ w przestrzeni czterowymiarowej. Grupa ta jest blisko związana z grupą obrotów SO³ przestrzeni trójwymiarowej. Przypiszmy mianowicie dowolnemu kwaternionowi h obrót T_h wg wzoru:

T_h(x) = hxh ^{− 1}.

Wówczas:

• przekształcenie T_h jest obrotem w trójwymiarowej przestrzeni kwaternionów urojonych.
• przekształcenie definiuje podwójne nakrycie grupy SO³ przez sferę S³.
• jeśli wyrazimy kwaternion h w postaci wykładniczej e^va, wtedy T_h jest obrotem wokół osi v kąt 2a.

Zastosowania

Kwaterniony są używane w grafice komputerowej do wykonywania obrotów w przestrzeni trójwymiarowej. Klasa obsługująca kwaterniony zdefiniowana jest w pakiecie DirectX ^[2]. Ich zastosowania w matematyce są jednak o wiele szersze.

Sam Hamilton używał kwaternionów do linearyzacji równań różniczkowych , m.in. w mechanice niebieskiej - obrót to pomnożenie przez stałe kwaterniony. Kwaternionów Hamiltona używa się do konstrukcji wiązek wektorowych w geometrii różniczkowej . Użyto ich też w teorii liczb do badania liczby przedstawień liczby naturalnej jako sumy czterech kwadratów liczb całkowitych (co akurat przydaje się w równaniach różniczkowych cząstkowych ).

Uogólnionych algebr kwaternionów używa się w teorii liczb (ładne sformułowanie zasady lokalno-globalnej Minkowskiego-Hasse), geometrii algebraicznej ( stożkowe jako rozmaitości Severi-Brauera); pojawiają się w teorii kohomologii Galois (kohomologii etalnych) jako elementy rzędu 2 w grupie Brauera ciała (słynne twierdzenie Merkurjewa z 1981 identyfikuje owe elementy rzędu dwa jako klasy iloczynów tensorowych uogólnionych algebr kwaternionów); algebraiczna K-teoria rzutowej krzywej stożkowej wyraża się przez algebraiczną K-teorię ciała współczynników i K-teorię odpowiedniej uogólnionej algebry kwaternionów. Ogólniej, R. Swan udowodnił w 1985 , że algebraiczna K-teoria kwadryki rzutowej wyraża się przez algebraiczne K-teorie ciała i odpowiedniej algebry Clifforda , która jest albo algebrą macierzy nad iloczynem tensorowym uogólnionych algebr kwaternionów, albo iloczynem kartezjańskim dwóch takich algebr (macierzy).

Zobacz też

• Oktawy Cayleya

Linki zewnętrzne

• kwaterniony w grafice komputerowej i mechanice (Gernot Hoffman)
• kalkulator dla kwaternionów

Bibliografia

• Wacław Sierpiński : Arytmetyka teoretyczna. PWN , 1968. 

Przypisy