Sortowanie szybkie
Rodzaj	Sortowanie
Struktura danych	Różne
Złożoność
Czasowa	О(n2)
Pamięciowa	zależnie od implementacji

Sortowanie szybkie ( ang. quicksort) – jeden z popularnych algorytmów sortowania działających na zasadzie " dziel i zwyciężaj ".

Sortowanie QuickSort zostało wynalezione w 1962 przez C.A.R. Hoare'a ^[1].

Zasada

Algorytm działa rekursywnie - wybierany jest pewien element tablicy, tzw. element osiowy, po czym na początek tablicy przenoszone są wszystkie elementy mniejsze od niego, na koniec wszystkie większe, a w powstałe między tymi obszarami puste miejsce trafia wybrany element. Potem sortuje się osobno początkową i końcową część tablicy. Rekursja kończy się, gdy kolejny fragment uzyskany z podziału zawiera pojedynczy element, jako że jednoelementowa podtablica nie wymaga sortowania.

Jeśli przez l oznacza się indeks pierwszego, a przez r – ostatniego elementu sortowanego fragmentu tablicy, zaś przez i – indeks elementu, na którym tablica została podzielona, to procedurę sortowania można (w dużym uproszczeniu) przedstawić następującym pseudokodem:

  PROCEDURE Quicksort(l, r)  BEGIN    IF l < r THEN                { jeśli fragment dłuższy niż 1 element }      BEGIN        i = PodzielTablice(l, r);  { podziel i zapamiętaj punkt podziału }        Quicksort(l, i-1);         { posortuj lewą część }        Quicksort(i, r);           { posortuj prawą część }      END  END

Algorytm sortowania szybkiego jest bardzo wydajny: jego średnia złożoność obliczeniowa jest rzędu 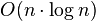(zob. hasło Notacja dużego O ). Jego szybkość i prostota implementacji powodują, że jest powszechnie używany; jego implementacje znajdują się również w standardowych bibliotekach języków programowania - na przykład w bibliotece standardowej języka C (funkcja qsort), w implementacji klasy TList w Delphi , jako procedura standardowa w PHP itp.

Złożoność

Algorytm ten dość dobrze działa w praktyce, ale ma bardzo złą pesymistyczną złożoność.

Przypadek optymistyczny

W przypadku optymistycznym, jeśli mamy szczęście za każdym razem wybrać medianę z sortowanego fragmentu tablicy, to liczba porównań niezbędnych do uporządkowania n-elementowej tablicy opisana jest rekurencyjnym wzorem

Dla dużych n:

co daje w rozwiązaniu liczbę porównań (a więc wskaźnik złożoności czasowej):

Równocześnie otrzymuje się minimalne zagnieżdżenie rekursji (czyli głębokość stosu, a co za tym idzie, złożoność pamięciową):

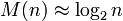
Przypadek przeciętny

W przypadku przeciętnym, to jest dla równomiernego rozkładu prawdopodobieństwa wyboru elementu z tablicy:

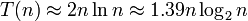
złożoność jest zaledwie o 39% wyższa, niż w przypadku optymistycznym.

Przypadek pesymistyczny

W przypadku pesymistycznym, jeśli zawsze wybierzemy element najmniejszy (albo największy) w sortowanym fragmencie tablicy, to:

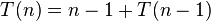
skąd wynika kwadratowa złożoność czasowa:

W tym przypadku otrzymuje się też olbrzymią, liniową złożoność pamięciową:

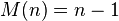
Usprawnienia algorytmu

Wybór elementu

Najprostsza, "naiwna" metoda podziału – wybieranie zawsze skrajnego elementu tablicy – dla danych już uporządkowanych daje katastrofalną złożoność O(n²). Trywialne na pozór zadanie posortowania posortowanej tablicy okazuje się dla tak zapisanego algorytmu zadaniem skrajnie trudnym. Aby uchronić się przed takim przypadkiem stosuje się najczęściej randomizację wyboru albo wybór "środkowy z trzech". Pierwszy sposób opiera się na losowaniu elementu osiowego, co sprowadza prawdopodobieństwo zajścia najgorszego przypadku do wartości zaniedbywalnie małych. Drugi sposób polega na wstępnym wyborze trzech elementów z rozpatrywanego fragmentu tablicy, i użyciu jako elementu osiowego tego z trzech, którego wartość leży pomiędzy wartościami pozostałych dwu. Można również uzupełnić algorytm o poszukiwanie przybliżonej mediany (patrz poniżej: Gwarancja złożoności).

Ograniczenie rekursji

Wysoka wydajność algorytmu sortowania szybkiego predestynuje go do przetwarzania dużych tablic. Takie zastosowanie wymaga jednak zwrócenia szczególnej uwagi na głębokość rekursji. Głębokość rekursji wiąże się bowiem z wykorzystaniem stosu maszynowego.

W najgorszym przypadku, jeśli algorytm będzie dzielił tablicę zawsze na część jednoelementową i resztę, to rekursja osiągnie głębokość n-1. Aby temu zapobiec, należy sprawdzać, która część jest krótsza – i tę porządkować najpierw. Z dłuższą zaś nie wchodzić w rekursję, lecz ponownie dzielić na tym samym poziomie wywołania:

  PROCEDURE Quicksort( l, r )  BEGIN    WHILE l < r DO                 { dopóki fragment dłuższy niż 1 element }    BEGIN      i := PodzielTablice( l, r );      IF (i-l) ≤ (r-i) THEN        { sprawdź, czy lewa część krótsza }        BEGIN                      { TAK? }          Quicksort( l, i-1 );     { posortuj lewą, krótszą część }          l := i+1                 { i kontynuuj dzielenie dłuższej }        END      ELSE        BEGIN                      { NIE }          Quicksort( i, r );       { posortuj prawą, krótszą część }          r := i-1                 { i kontynuuj dzielenie dłuższej }        END    END  END

Przy takiej organizacji pracy na stosie zawsze pozostają zapamiętane (w zmiennych i, r albo l, i) indeksy ograniczające dłuższą, jeszcze nie posortowaną część tablicy, a wywołanie rekurencyjne zajmuje się częścią krótszą. To znaczy, że na każdym poziomie wywołań algorytm obsługuje fragment będący co najwyżej połową fragmentu z poprzedniego poziomu. Stąd wynika, że poziomów wywołań nie będzie więcej, niż log₂n, gdzie n oznacza długość całej tablicy. Zatem usprawnienie to zmienia asymptotyczne wykorzystanie pamięci tego algorytmu z O(n) do O(log₂n).

Quicksort w miejscu

Istnieje modyfikacja czyniąca algorytm quicksort działającym w miejscu . W oryginalnym sortowaniu szybkim używa się rekursji lub stosu (de facto oba sposoby niewiele się różnią – rekursja w uproszczeniu jest niejawnym stosem) do zapamiętywania miejsc podziału. Więc chociaż algorytm w obu wersjach nie korzysta z dodatkowych tablic o rozmiarze zależnym od rozmiaru danych wejściowych, to nie można nazywać go działającym w miejscu, gdyż wysokość, a więc i wymagania pamięciowe wywołań rekursji/stosu są ściśle zależne od rozmiaru danych początkowych.

Załóżmy, że dla sortowanej tablicy A funkcja PodzielTablice(l,p) zwróciła wartość s. W oryginalnym algorytmie quicksort powinno zostać wykonane wywołania Quicksort(l,s-1) i Quicksort(s+1,p). Zamiast tego "zajmujemy się" tylko Quicksort(l,s-1), a pozycje s+1 i p zapamiętujemy w następujący sposób:

• s+1: jest jednoznacznie wyznaczona przez koniec ciągu (l,s-1) → (s+1) = (s-1) + 2
• p: znajdujemy maksimum ciągu (s+1,p) i zamieniamy tę pozycję z pozycją s. Aby odtworzyć pozycję p, wystarczy przeszukiwać ciąg w prawo do znalezienia elementu większego od wartości stojącej na pozycji s. Wtedy indeks elementu o najmniejszej wartości większej od A[s] to p+1.

Metoda ta sprowadza koszt pamięciowy algorytmu do wartości stałej, O(1), wymaga jednak dodatkowego nakładu czasu na wyszukiwanie maksymalnych elementów kolejno sortowanych fragmentów tablicy. Ujmuje więc algorytmowi jego główną zaletę, wpisaną nawet w jego nazwę – szybkość działania.

Drobne fragmenty

U podstaw kolejnego usprawnienia leży spostrzeżenie, że około połowa wszystkich rekurencyjnych wywołań procedury dotyczy jednoelementowych fragmentów tablicy – a więc fragmentów z definicji posortowanych. Co więcej, po wliczeniu dodatkowej pracy potrzebnej na wybór elementu dzielącego i zorganizowanie pętli dzielącej tablicę okazuje się, że sortowanie tablic nawet kilkuelementowych algorytmem quicksort jest bardziej pracochłonne, niż jakimś algorytmem prostym, na przykład przez wstawianie .

Warto więc zaniechać dalszych podziałów, gdy uzyskane fragmenty staną się dostatecznie krótkie – rzędu kilku lub kilkunastu elementów. Otrzymuje się w wyniku tablicę "prawie posortowaną", w której większość elementów może nie znajduje się na właściwych miejscach, ale są blisko właściwych miejsc. Taką tablicę ostatecznie sortuje się algorytmem wstawiania , który bardzo efektywnie radzi sobie z tego rodzaju danymi. Jak pokazuje praktyka, wybór granicznej długości fragmentu (progu "odcięcia" rekursji, ang. cutoff) nie wymaga szczególnych rygorów – algorytm działa niemal równie dobrze dla wartości od 5 do 25. W większości zastosowań pozwala to osiągnąć oszczędność łącznego czasu wykonania rzędu 20% ^[2].

Gwarancja złożoności

Pomimo wszelkich usprawnień, pozostaje jednak, zazwyczaj znikome, prawdopodobieństwo zajścia przypadku pesymistycznego, w którym złożoność czasowa wynosi O(n²). Jeśli chcemy mieć pewność wykonania sortowania w czasie nie dłuższym niż O(nlog₂n), należy uzupełnić algorytm o poszukiwanie przybliżonej mediany , czyli elementu dzielącego posortowaną tablicę na tyle dobrze, że pesymistyczne oszacowanie złożoności zrówna się z optymistycznym.

Jeżeli prawdopodobieństwo wystąpienia przypadku pesymistycznego w praktyce jest duże, to można skorzystać ze specjalnych algorytmów znajdowania dobrej mediany. Niestety algorytmy te mają dość dużą złożoność, dlatego w takiej sytuacji należy też rozważyć skorzystanie z innych algorytmów sortowania, takich jak np. sortowanie stogowe (ang. heap sort), sortowanie pozycyjne (radix sort), czy sortowanie przez scalanie (mergesort).

W większości praktycznych zastosowań algorytm sortowania szybkiego jest bezkonkurencyjny. W praktyce pozostaje on zdecydowanie najczęściej używanym algorytmem sortowania. Opracowano też wiele modyfikacji i usprawnień tego algorytmu, poprawiając niektóre właściwości, lub dostosowując go do konkretnych wymagań.

Wadą sortowania szybkiego jest brak stabilności. Z tego powodu w niektórych zastosowaniach jest używany mergesort .

Przykładowe implementacje

Wikiźródła

Zobacz przykładowe implementacje sortowania szybkiego na Wikiźródłach

Przypisy

Zobacz też

• sortowanie