Rozkład prawdopodobieństwa

Rozkład prawdopodobieństwa

Rozkład prawdopodobieństwa – w najczęstszej interpretacji (rozkład zmiennej losowej) miara probabilistyczna określona na sigma-ciele podzbiorów zbioru wartości zmiennej losowej ( wektora losowego ), pozwalająca przypisywać prawdopodobieństwa zbiorom wartości tej zmiennej, odpowiadającym zdarzeniom losowym . Formalnie rozkład prawdopodobieństwa może być jednak rozpatrywany także bez stosowania zmiennych losowych.

Spis treści

1 Definicja
2 Zastosowanie dla zmiennych losowych
- 2.1 Rozkład ciągły
- 2.2 Rozkład dyskretny
3 Dystrybuanta
- 3.1 Dystrybuanta rozkładu jednowymiarowego
  - 3.1.1 Przykład
- 3.2 Dystrybuanta rozkładu wielowymiarowego
4 Dodatkowe definicje
5 Popularne rozkłady
- 5.1 Rozkłady ciągłe
- 5.2 Rozkłady dyskretne
6 Statystyka
7 Przypisy
8 Zobacz też

Definicja

Rozkładem prawdopodobieństwa nazywa się dowolną miarę probabilistyczną $P\;$ określoną na σ-ciele podzbiorów borelowskich pewnej przestrzeni polskiej . Dla rozkładów ciągłych często jest nią zbiór liczb rzeczywistych $\mathbb R$ (tzw. rozkład jednowymiarowy) lub przestrzeń euklidesowa $\mathbb{R}^n$ dla pewnej liczby naturalnej $n\;$ (rozkład wielowymiarowy).

Zastosowanie dla zmiennych losowych

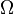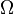Zwykle rozważa się tzw. przestrzeń probabilistyczną , złożoną z przestrzeni zdarzeń elementarnych $\Omega\;$ , określonego na niej σ-ciała $\mathcal F$ , którego elementy są nazywane zdarzeniami losowymi, oraz miary probabilistycznej $P\;$ , przyporządkowującej zdarzeniom liczby zwane prawdopodobieństwami. Tak określone prawdopodobieństwa są jednak niewygodne do badania, gdyż $\Omega\;$ może być dowolnym zbiorem, nawet bez zadanych jakichkolwiek relacji między jego elementami.

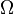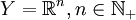Wprowadza się zatem funkcję mierzalną zwaną zmienną losową , która przyporządkowuje elementom przestrzeni zdarzeń elementarnych $\Omega\;$ elementy pewnej przestrzeni mierzalnej $Y\;$ o pożądanych właściwościach^[1]. Najczęściej wykorzystuje się przestrzeń euklidesową $Y=\mathbb R^n, n\in\mathbb N_{+}\;$ a zmienną nazywa się wówczas wektorem losowym . Czasem miano zmiennej losowej rezerwuje się tylko dla przypadku jednowymiarowego $Y=\mathbb R\;$ .

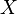Obrazem każdego zdarzenia losowego (elementu rodziny $\mathcal F$ ) poprzez zmienną losową $X\;$ jest mierzalny podzbiór $Y\;$ . Mierzalne podzbiory $Y\;$ tworzą także σ-ciało $\mathcal B(Y)\;$ . Ponieważ zmienna losowa nie musi być funkcją różnowartościową , więc ten sam zbiór mierzalny $A\in\mathcal B(Y)\;$ można w ogólnym przypadku otrzymać z wielu różnych zdarzeń o różnych prawdopodobieństwach. Aksjomaty σ-ciała zapewniają, że wśród tych zdarzeń jest także ich suma i do niej jest przypisane największe prawdopodobieństwo. Suma ta jest równa przeciwobrazowi zbioru $A\;$ , czyli $X^{-1}(A)\;$ .

Rozkład zmiennej losowej 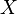$X\;$ to funkcja $P_X\;$ określona na $\mathcal B(Y)\;$ wzorem $P_X(A) = P (X^{-1}(A)),\ A\in \mathcal B(Y)\;$ .

Rozkład $P_X\;$ jest nową miarą probabilistyczną. Jest on w przestrzeni stanów $Y\;$ odpowiednikiem miary probabilistycznej $P\;$ .
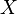Uwaga: Zapis $P_X\;$ gdzie $X\;$ jest zdarzeniem a nie zmienną losową jest stosowany na oznaczenie prawdopodobieństwa warunkowego .

Wyróżnia się niżej omówione rozkłady ciągłe i dyskretne, jednak należy pamiętać, iż oprócz nich istnieją także rozkłady nie mieszczące się w żadnej z tych kategorii – na przykład rozkład o dystrybuancie Cantora .

Rozkład ciągły

Jeżeli istnieje funkcja $f\colon Y\to [0,\infty)\;$ , taka że

$P(A)=\int\limits_A~f(x)\;dx$

( całka Lebesgue'a ) dla dowolnego zbioru borelowskiego $A \in \mathcal B(Y)$ , to funkcję tę nazywa się gęstością (rozkładu) prawdopodobieństwa lub funkcją gęstości prawdopodobieństwa. Nazwa pochodzi od intuicji fizycznych, zob. gęstość masy . O rozkładzie $P\;$ mającym gęstość mówi się, że jest ciągły (lub typu ciągłego).

Powyższa definicja jest poprawna dla dowolnych rozkładów prawdopodobieństwa, także wielowymiarowych – wówczas 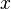$x\;$ jest wektorem.

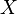Rozkład $P_X\;$ zmiennej losowej $X\;$ spełniający powyższe warunki definiuje się analogicznie. O zmiennej losowej również mówi się wówczas, iż jest ciągła (lub typu ciągłego).

Rozkład dyskretny

Rozkład $P$ nazywa się dyskretnym, jeśli jest skupiony na zbiorze przeliczalnym, tzn. istnieje zbiór (co najwyżej) przeliczalny $S \subseteq Y$ dla którego $P (S) = 1$ . Jeżeli

$S = \{s_i\colon i \in I\}$ oraz

p i = P ({s i})

dla każdego $i \in I$ ,

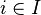to dla dowolnego zbioru borelowskiego $A$

$P(A) = P(A \cap S) = \sum_{i \in I}~p_i \boldsymbol 1_A(s_i)$ ,

gdzie $\boldsymbol 1_A$ to indykator (funkcja charakterystyczna) zbioru $A$ .

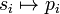Zatem zbiór par $\{(s_i, p_i)\colon i \in I\}$ jednoznacznie wyznacza rozkład $P$ . Stąd dowolny zbiór tej postaci, gdzie $p i > 0$ oraz $\sum p_i = 1$ (co wynika z własności rozkładu), nazywa się czasami rozkładem (dyskretnym). Odwzorowanie $s_i \mapsto p_i$ , oznaczane $\operatorname{pmf}(s_i) = p_i$ , nosi nazwę funkcji masy prawdopodobieństwa i jest ono dyskretnym odpowiednikiem gęstości prawdopodobieństwa.

Dyskretna zmienna losowa $X$ to zmienna losowa o rozkładzie dyskretnym. Wówczas można go zdefiniować podobnie jak wyżej równością

P X ({x i}) = P (X - 1 (A))

jednakże w tym wypadku zachodzi dodatkowo

$P (X^{-1}(A)) = P (\{\omega \in \Omega\colon X(\omega) = x_i\}) \overset\underset\mathrm{ozn}\ {=} P (X = x_i) \overset\underset\mathrm{ozn}\ {=} \operatorname{pmf}_X(x_i)$ ,

gdzie $\left\{x_i\right\}_{i \in I}$ jest zbiorem wszystkich wartości przyjmowanych przez zmienną $X$ .

Dystrybuanta

Badanie rozkładu jako miary jest zadaniem dość trudnym, jednak można je znacząco uprościć wprowadzając funkcję dystrybuanty, która całkowicie go opisuje i jest funkcją przestrzeni euklidesowej w przedział $[0,1]$ .

Dystrybuanta rozkładu jednowymiarowego

Dystrybuanta jednowymiarowego rozkładu (prawdopodobieństwa) $P\;$ to funkcja $F_P\colon \mathbb R \to \mathbb R$ , zdefiniowana wzorem:

$F_P(t) = P((-\infty, t])$ .

Dystrybuanta (rozkładu) zmiennej losowej 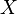$X\;$ , to dystrybuanta $F_{P_X}\;$ , oznaczana zwykle symbolem $F_X\;$ , otrzymana z rozkładu tej zmiennej losowej:

$F_X(t) = P_X(\{x\colon x \leqslant t\})$

Dystrybuanta w pełni wyznacza rozkład, tzn. dwie zmienne o tej samej dystrybuancie muszą mieć ten sam rozkład; obrazuje to poniższy przykład.

Jeśli rozkład $P\;$ ma gęstość $f\;$ , jego dystrubuanta $F_P\;$ wyraża się wzorem:

$F_P(t) = \int\limits_{-\infty}^t~f(x)\;dx$ .

Przykład

Niech $\Omega_1 = \{\mathrm O, \mathrm R\}\;$ będzie modelem doświadczenia losowego polegającego na rzucie monetą, które może z jednakowym prawdopodobieństwem dać dwa wyniki: orła i reszkę. Stąd

$P (\mathrm O) = \tfrac{1}{2}$ oraz $P (\mathrm R) = \tfrac{1}{2}$ .

Jeżeli zmienna 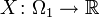$X\colon \Omega_1 \to \mathbb R$ jest określona równościami

$X(\mathrm O) = -1\;$ oraz $X(\mathrm R) = 1\;$ ,

to jej rozkład $P_X\;$ jest określony następująco:

$P (X \in A) = \begin{cases} 0, & \mbox{dla } A = \mathbb R \setminus \{-1, 1\} \\ \tfrac{1}{2}, & \mbox{dla } A = \{-1\} \mbox{ lub } A = \{1\} \\ 1, & \mbox{dla } A = \{-1, 1\} \end{cases}$ ,

funkcja masy prawdopodobieństwa ma z kolei postać:

$P (X = x) = \begin{cases} 0, & \mbox{dla } x \ne -1\ \mbox{ i }\ \ x \ne 1 \\ \tfrac{1}{2}, & \mbox{dla } x = -1 \mbox{ lub } x = 1 \end{cases}$ ,

co oznacza, że zmienna losowa 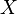$X\;$ odwzorowuje zdarzenia

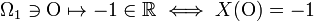$\Omega_1 \ni \mathrm O \mapsto -1 \in \mathbb R \iff X(\mathrm O) = -1$ ,

$\Omega_1 \ni \mathrm R \mapsto \,\ \ 1 \in \mathbb R \iff X(\mathrm R) = \,\ \ 1$

oraz zachowuje prawdopodobieństwo określone na $(\Omega_1, \mathcal F)$ przekształcając je w rozkład określony na $(\mathbb R, \mathcal B(\mathbb R))$ .

Niech $\Omega_2 = \{\mathrm O, \mathrm R, \mathrm K\;$ będzie modelem opisującym jak wyżej rzut monetą poszerzone o dodatkowy wynik: upadek na kant, który prawie na pewno się nie zdarzy. Jeżeli

$P (\mathrm O) = P (\mathrm R) = \tfrac{1}{2}$ oraz $P (\mathrm K) = 0\;$ ,

to zmienna losowa $Y\colon \Omega_2 \to \mathbb R$ określona równościami

$Y(\mathrm O) = -1,\; Y(\mathrm R) = 1$ oraz $Y(\mathrm K) = 7\;$ ,

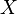będzie miała taki sam rozkład $P_Y\;$ (oraz funkcję masy) co zmienna $X\;$ określona wyżej, mimo iż są one różne.

Z definicji dystrybuanty wynika, iż prawdopodobieństwo zdarzenia

$A = \{\omega \in \Omega\colon a < X(\omega) \leqslant b\} \overset\underset\mathrm{ozn}\ {=} \{a < X \leqslant b\}$

dane jest wzorem

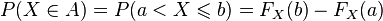$P (X \in A) = P (a < X \leqslant b) = F_X(b) - F_X(a)$ .

Dystrybuanta zmiennej 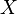$X\;$ to funkcja $F_X\colon \mathbb R \to [0, 1]$ określona wzorem

$F_X(t) = \begin{cases} 0, & \mbox{dla } t \leqslant -1 \\ \tfrac{1}{2}, & \mbox{dla } -1 < t \leqslant 1 \\ 1, & \mbox{dla } t > 1. \end{cases}$

Warto zauważyć, iż dystrybuanta $F_Y\;$ zmiennej $Y\;$ dana jest tym samym wzorem co dystrybuanta $F_X\;$ .

Dystrybuanta rozkładu wielowymiarowego

Jeśli 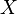$X\;$ jest wektorem losowym , tzn. $X\colon \Omega \to \mathbb R^n$ , to zmienia się nieco postać dystrybuanty. Rozważa się wówczas przedziały wielowymiarowe, tzn. zbiory będące iloczynami kartezjańskimi przedziałów prostej postaci

$(-\infty, t_1] \times (-\infty, t_2] \times \dots \times (-\infty, t_n]$ ;

dystrybuanta $F_P\colon \mathbb R^n \to \mathbb R$ takiego zdarzenia zapisywana jest zwykle jako

$F_P(t_1, t_2, \dots, t_n) = P((-\infty, t_1] \times (-\infty, t_2] \times \dots \times (-\infty, t_n])$ .

Stosuje się następujący zapis dystrybuanty rozkładu zmiennej losowej:

$F_X(t_1, t_2, \dots, t_n) = P (\{X\colon X_1 \leqslant t_1\wedge X_2 \leqslant t_2 \wedge \dots \wedge X_n \leqslant t_n\})$ ,

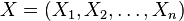gdzie $X = (X_1, X_2, \dots, X_n)$ . Jeżeli przyjmie się $t = (t_1, t_2, \dots, t_n)$ , to zapis

$F_X(t) = P (X \leqslant t)$

nie prowadzi zwykle do większych nieporozumień.

Jeśli rozkład wielowymiarowy $P\;$ ma gęstość $f\;$ , jego dystrybuanta $F_P\;$ wyraża się wzorem (całka Lebesgue'a):

$F_P(t) = \int\limits_{(-\infty, t_1] \times (-\infty, t_2] \times \dots \times (-\infty, t_n]}~f(t)\;dt$ .

Zwykle wzór ten spotyka się w prostszej wersji, choć o mniejszym zakresie stosowalności (nie każdą całkę Lebesgue'a da się w ten sposób rozbić):

$F_P(t) = \int\limits_{-\infty}^{t_1}\int\limits_{-\infty}^{t_2}\cdots\int\limits_{-\infty}^{t_n} f(t_1,t_2,\dots,t_n) dt_n \dots dt_2 dt_1$

Dodatkowe definicje

Zmienna losowa 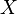$X\;$ ma rozkład osobliwy (singularny), jeśli ma ciągłą dystrybuantę i istnieje zbiór 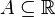$A \subseteq \mathbb R$ , który ma zerową miarę Lebesgue'a , ale jednostkowy rozkład (miarę) prawdopodobieństwa, tzn. $\lambda(A) = 0\;$ oraz $P(A) = 1\;$

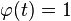Rozkłady skoncentrowane na zbiorze punktów postaci $kc\;$ , gdzie $k \in \mathbb Z$ nazywa się arytmetycznymi. To, iż rozkład $P\;$ jest skupiony na zbiorze $\left\{\tfrac{2\pi k}{t} \colon k \in \mathbb Z\right\}$ jest równoważne temu, iż jego funkcja charakterystyczna $\varphi$ ma okres równy $t\;$ bądź $\varphi(t) = 1\;$ dla pewnego $t \ne 0\;$ . Z obserwacji funkcji charakterystycznych wynika, iż arytmetyczne są rozkłady: geometryczny, Bernoulliego i Poissona; rozkłady jedno- i dwupunktowe są przesuniętymi rozkładami tego typu.

Popularne rozkłady

Rozkłady ciągłe

Wybrane rozkłady gęstości prawdopodobieństwa:
ƒ_N(x) – rozkład normalny ,
ƒ_E(x) – rozkład wykładniczy ,
ƒ_R(x) – rozkład jednostajny ,
ƒ_T(x) – rozkład trójkątny ,
ƒ_D(x)– rozkład delty Diraca dla zmiennej pewnej.

rozkład beta ,
rozkład χ² ,
rozkład Cauchy'ego ,
rozkład Erlanga ,
rozkład F Snedecora ,
rozkład gamma ,
rozkład Gumbela ,
rozkład Weibulla ,
rozkład jednostajny ciągły (prostokątny),
rozkład Laplace'a,
rozkład Leviego,
rozkład logarytmiczno-normalny ,
rozkład normalny (Gaussa),
rozkład normalny wielowymiarowy ,
rozkład trójkątny ,
rozkład t-Studenta ,
rozkład wykładniczy .

Rozkłady dyskretne

rozkład Boltzmanna ,
rozkład dwupunktowy (Bernoulliego u anglojęzycznych autorów),
rozkład dwumianowy (Bernoulliego u większości polskich autorów),
rozkład jednopunktowy (typu delta Diraca ),
rozkład jednostajny dyskretny ,
rozkład geometryczny ,
rozkład hipergeometryczny ,
rozkład Poissona ,
rozkład zero-jedynkowy ,
rozkład ujemny dwumianowy (Pascala).

Statystyka

Jeśli mamy na myśli rzeczywiste prawdopodobieństwa wystąpienia danej wartości cechy w populacji , to mówimy o rozkładzie w populacji. Jeśli mamy na myśli prawdopodobieństwa wystąpienia danej cechy wyznaczone podczas badania statystycznego , to mówimy o rozkładzie empirycznym .

Przypisy

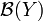↑ Ściślej musi to być funkcja $\mathcal{F}/\mathcal{B}(Y)$ -mierzalna, gdzie $\mathcal{B}(Y)$ jest rodziną podzbiorów borelowskich przestrzeni $Y\;$ . Jako $Y\;$ zwykle wybiera się jedną z tzw. przestrzeni polskich , do których zaliczają się w szczególności przestrzenie euklidesowe.

Zobacz też

Inne hasła zawierające informacje o "Rozkład prawdopodobieństwa":

Oddychanie komórkowe ...

Eunectes ...

Wodorotlenek wapnia ...

Ekologia ...

Ekosystem ...

Celuloza ...

Rawicz (herb szlachecki) ...

Zasada trzech jedności ...

Bajkał ...

Wrocław ...

Inne lekcje zawierające informacje o "Rozkład prawdopodobieństwa":

223 Czas przełomu (plansza 7) ...

Składniki powietrza (plansza 11) ...

032 Najazdy mongolskie w XIII w. (plansza 10) ...

Publikacje nauczycieli

Logowanie i rejestracja

Załóż nowe konto za darmo » Odzyskaj stracone hasło

Czy wiesz, że...

Zasolenie wody w oceanach wynosi od 30 do 38 promili (3,0% do 3,8%).

woda promil ocean

Rodzaje szkół

AP Edukacja - licea
i szkoły policealne

Publikacje nauczycieli

Kontakt

Formularz dodania
szkoły do katalogu

Ogólnopolski Katalog Szkolnictwa
www.szkolnictwo.pl
ul. Kaszubska 10/16
75-036 Koszalin

Wszelkie pytania, uwagi i zmiany w katalogu prosimy kierować do:

	zmiany@szkolnictwo.pl

Wszelkie pytania, uwagi dotyczące Platformy Edukacyjnej prosimy kierować do:

	platforma@szkolnictwo.pl

Konta bankowe dla klientów katalogu szkolnictwo.pl:

Pełny ekran >>>

Wiadomości

Reklama

zamów reklamę >>>

Dodaj szkołę

Formularz dodania
szkoły do katalogu

Nauka

	Język angielski
Słówka - testy Słówka - lekcje Testy po angielsku Gimnazjum - lekcje Gimnazjum - testy do lekcji Liceum - lekcje Liceum - testy do lekcji

	Testy na prawo jazdy
Kategoria B - lekcje Kategoria B - testy do lekcji Testy do egzaminu

	Język niemiecki
Słówka - testy Słówka - lekcje Gimnazjum - lekcje Gimnazjum - testy do lekcji Liceum - lekcje Liceum - testy do lekcji

	Matematyka
Gimnazjum - lekcje Gimnazjum - testy do lekcji Liceum - lekcje Liceum - testy do lekcji Konkurs "Kangur Matematyczny"

	Geografia
Gimnazjum - lekcje Gimnazjum - testy do lekcji Liceum - lekcje Liceum - testy do lekcji Państwa świata

	Chemia
Gimnazjum - lekcje Gimnazjum - testy do lekcji Liceum - lekcje Liceum - testy do lekcji

	Język hiszpański
Słówka

	Prawo
Egzamin konkursowy dla kandydatów na aplikantów

	Język polski
Liceum - lekcje Liceum - testy do lekcji Liceum - testy do lektur Gimnazjum - lekcje Gimnazjum - testy do lekcji Ortografia - testy

	Historia
Liceum - lekcje Liceum - testy do lekcji Gimnazjum - lekcje Gimnazjum - testy do lekcji

	Biologia
Gimnazjum - lekcje Gimnazjum - testy do lekcji Liceum - lekcje Liceum - testy do lekcji

	Fizyka i astronomia
Zadania do matury Gimnazjum - lekcje Gimnazjum - testy do lekcji Liceum - lekcje Liceum - testy do lekcji

	Informatyka
Informatyka - zadania do matury Gimnazjum - lekcje Gimnazjum - testy do lekcji Liceum - lekcje Liceum - testy do lekcji

	Wiedza o społeczeństwie
Liceum - lekcje Liceum - testy do lekcji

	Podstawy przedsiębiorczości
Liceum - lekcje Liceum - testy do lekcji

	Język angielski
	Filozofia
	Testy na prawo jazdy
	Język niemiecki
	Matematyka
	Geografia
	Chemia
	Język hiszpański
	Prawo
	Język polski
	Historia
	Biologia
	Fizyka i astronomia
	Informatyka
	Wiedza o społeczeństwie
	Podstawy przedsiębiorczości
	Egzaminy Zawodowe
	Materiały szkół