Równania Eulera-Lagrange'a

Równania Eulera-Lagrange\'a

Równania Eulera-Lagrange'a wprowadzone przez Leonharda Eulera i Josepha Louisa Lagrange'a w 1750 roku są podstawową formułą rachunku wariacyjnego .

W mechanice klasycznej opisują one ruch $q k (t)$ układu ciał i przyjmują postać

$\frac{d}{dt} \left (\frac{\partial L}{\partial \dot{q} _{k}}\right ) - \frac{\partial L}{\partial q _{k}} = 0$

gdzie $L(q _{1}, \ldots, q_{n}; \dot{q} _{1}, \ldots, \dot{q} _{n}; t)$ jest funkcją Lagrange'a ( lagranżjanem ) opisującą rozważany układ.

Otrzymujemy je z zasady najmniejszego działania i dla znanej funkcji Lagrange'a są one układem n równań różniczkowych zwyczajnych na funkcje $q k (t)$ .

Wyrażenia występujące w równaniach Eulera-Lagrange'a mają swoje nazwy:

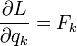$\frac{\partial L}{\partial q _{k}} = F_{k}$ - siła uogólniona

$\frac{\partial L}{\partial \dot{q} _{k}} = p_{k}$ - pęd uogólniony

Przykładowe rozwiązanie

Weźmy lagranżjan postaci:

$L(x,\dot{x}) = \frac{m \dot{x} ^{2} }{2} - V(x)$

Poszczególne wyrazy w równaniu Eulera-Lagrange'a wynoszą:

$\frac{\partial L}{\partial x} = -\frac{\partial V(x)}{\partial x}$

$\frac{\partial L}{\partial \dot{x}} = m \dot{x}$

$\frac{d}{dt} \left (\frac{\partial L}{\partial \dot{x}}\right ) = m\ddot{x}$

Ostatecznie otrzymujemy:

$m\ddot{x} = -\frac{\partial V(x)}{\partial x}$

czyli równanie ruchu Newtona:

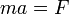
$\left. ma = F \right.$

gdyż dla sił potencjalnych $F = -\frac{\partial V(x)}{\partial x}$

Wyprowadzenie równań Eulera-Lagrange'a

Lemat: Jeżeli $b (t)$ jest funkcją ciągłą na $[t 1, t 2]$ i całka $\int\limits ^{t_{2}} _{t_{1}} b(t)h(t)dt$ znika dla dowolnej funkcji ciągłej h(t) posiadającej ciągłą pochodną i spełniającej warunek $h (t 1) = h (t 2) = 0$ to $b(t)\equiv 0$ dla $t \in [t_{1}, t_{2}]$ .

Będziemy szukać ekstremum funkcjonału działania.

$S[\bar{q}] = \int\limits ^{t_{2}} _{t_{1}} L(q_{1},\ldots,q_{n};\dot{q}_{1},\ldots,\dot{q}_{n},t)dt$

Warunkiem koniecznym, aby funkcjonał przyjmował wartość minimalną jest zerowanie pierwszej wariacji tego funkcjonału.

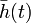Do funkcji $\bar{q}(t)$ dodajemy dowolne $\bar{h}(t)$ , spełniające warunek: $\bar{h}(t_{1}) = \bar{h}(t_{2}) = 0$

$\delta S[\bar{q}] = S[\bar{q}+\bar{h}] - S[\bar{q}] =$ $\int\limits ^{t_{2}} _{t_{1}} \left[L(q_{1}+h_{1},\ldots,q_{n}+h_{n};\dot{q}_{1}+\dot{h}_{1},\ldots,\dot{q}_{n}+\dot{h}_{n},t)\right.$ $\left.- L(q_{1},\ldots,q_{n};\dot{q}_{1},\ldots,\dot{q}_{n},t) \right]dt = 0$

Wyrażenie podcałkowe jest wariacją L $δ L$ .

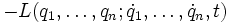
$\delta L = L(q_{1}+h_{1},\ldots,q_{n}+h_{n};\dot{q}_{1}+\dot{h}_{1},\ldots,\dot{q}_{n}+\dot{h}_{n},t)$ $- L(q_{1},\ldots,q_{n};\dot{q}_{1},\ldots,\dot{q}_{n},t)$

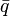W powyższym wzorze wyraz zależny od $\bar{q} + \bar{h}$ możemy rozwinąć w szereg Taylora wokół $\bar{q}$ odrzucając wyrazy powyżej pierwszego rzędu otrzymujemy:

$\delta L = \sum _{k=1} ^{n} \left [ h_{k}\frac{\partial L(q_{1},\ldots,q_{n};\dot{q}_{1},\ldots,\dot{q}_{n},t)}{\partial q_{k}} + \dot{h}_{k} \frac{\partial L(q_{1},\ldots,q_{n};\dot{q}_{1},\ldots,\dot{q}_{n},t)}{\partial \dot{q}_{k}}\right]$

Wstawiając powyższe równanie do wyrażenia podcałkowego otrzymujemy:

$\delta S[\bar{q}] = \int\limits ^{t_{2}} _{t_{1}} \sum _{k=1} ^{n} \left [ h_{k}\frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial q_{k}} + \dot{h}_{k} \frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial \dot{q}_{k}}\right] dt$

Scałkujmy przez części wyrażenia postaci $\dot{h}_{k} \frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial \dot{q}_{k}}$

$\int\limits ^{t_{2}} _{t_{1}} \dot{h}_{k} \frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial \dot{q}_{k}} dt = \left. h_{k} \frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial \dot{q}_{k}} \right | ^{t_{2}} _{t_{1}} - \int\limits ^{t_{2}} _{t_{1}} h_{k} \frac{d}{dt}\left( \frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial \dot{q}_{k}} \right)dt$

Z założenia o funkcji $h (t)$ wynika, że pierwsze wyrażenie po prawej stronie wynosi 0. Otrzymujemy poniższy wzór na wariację działania:

$\delta S[\bar{q}] = \int\limits ^{t_{2}} _{t_{1}} \sum _{k=1} ^{n} h_{k} \left [\frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial q_{k}} - \frac{d}{dt}\left( \frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial \dot{q}_{k}}\right) \right] dt$

Wyrażenie podcałkowe jest iloczynem skalarnym wektora 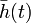$\bar{h}(t)$ i wektora złożonego z pochodnych funkcji L ( 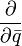$\frac{\partial}{\partial \bar{q}}$ oznacza $\nabla_{\bar{q}}$ , tzw. operator nabla ).

$\delta S[\bar{q}] = \int\limits ^{t_{2}} _{t_{1}} \bar{h} \cdot \left [\frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial \bar{q}} - \frac{d}{dt}\left( \frac{\partial L(\bar{q},\dot{\bar{q}},t)}{\partial \dot{\bar{q}}}\right) \right] dt$

Na podstawie lematu wnioskujemy, że wyrażenie w nawiasie kwadratowym się zeruje co daje układ równań Eulera-Lagrange'a.

Inne hasła zawierające informacje o "Równania Eulera-Lagrange'a":

Wystąpił problem z bazą danych. Spróbuj ponownie poprzez naciśnięcie przycisku "Odśwież".

Przepraszamy za powstały problem.

www.szkolnictwo.pl

Równania Eulera-Lagrange\'a

Przykładowe rozwiązanie

Wyprowadzenie równań Eulera-Lagrange'a