Funkcja ciągła –
funkcja
o następującej intuicyjnej własności: „mała” zmiana argumentu niesie ze sobą „małą” zmianę wartości; lub też: wartości funkcji dla „bliskich” sobie argumentów również będą sobie „bliskie”.
Funkcja rzeczywista
zmiennej rzeczywistej może być postrzegana jako ciągła, jeżeli jej
wykres
można „narysować bez odrywania ołówka od papieru” (bez ograniczeń w czasie lub przestrzeni). Jest to warunek wystarczający, ale nie konieczny. Funkcja f(x) = tan(x) jest ciągła mimo, że nie da jej się narysować zgodnie z podaną intuicją.
Funkcje rzeczywiste
Dla funkcji rzeczywistych zmiennej rzeczywistej istnieją dwie równoważne definicje ciągłości: jedna z nich podana przez
Augustina Louisa Cauchy'ego
, nazywana popularnie epsilonowo-deltową z racji przyjętych zwyczajowych oznaczeń; druga zaproponowana przez
Heinricha Eduarda Heinego
, nazywana też definicją ciągową. Niech  oraz
oraz  .
.
Definicja Cauchy'ego
Jeżeli f spełnia dla ustalonego 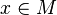 warunek
warunek
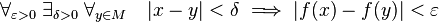 ,
,
to jest ona ciągła w sensie Cauchy'ego w punkcie x. Jeżeli spełnia ona powyższy warunek dla każdego 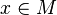 , czyli
, czyli
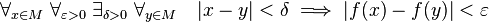 ,
,
to mówimy, że jest ciągła (w sensie Cauchy'ego) na zbiorze M.
Definicja Heinego
Funkcja f jest ciągła w sensie Heinego w punkcie 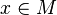 , jeśli dla każdego
ciągu
(xn) liczb z M, który jest
zbieżny
do x ciąg wartości
, jeśli dla każdego
ciągu
(xn) liczb z M, który jest
zbieżny
do x ciąg wartości  jest zbieżny do f(x), czyli
jest zbieżny do f(x), czyli
 .
.
Uwagi
Warto zauważyć, że z obiema definicjami ciągłości funkcji w punkcie są związane odpowiednie definicje
granicy funkcji
w punkcie. Używając pojęcia granicy funkcji możemy powiedzieć, że funkcja f jest ciągła w punkcie  , gdy albo x nie jest
punktem skupienia
zbioru M, albo
, gdy albo x nie jest
punktem skupienia
zbioru M, albo 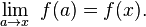
Należy także zwracać bacznie uwagę na kolejność
kwantyfikatorów
we wzorze na ciągłość w sensie Cauchy'ego dla danego zbioru. Przesunięcie pierwszego kwantyfikatora na trzecią pozycję, mianowicie
 ,
,
prowadzi do sformułowania o wiele silniejszej własności, tzw.
ciągłości jednostajnej
.
Obie definicje (Cauchy'ego i Heinego) są równoważne już przy założeniu bardzo słabej wersji
aksjomatu wyboru
, i nie jest on potrzebny dla dowodu równoważności globalnej ciągłości w odpowiednich znaczeniach.
Ciągłość jednostronna
Rozpatruje się czasami funkcje ciągłe jednostronnie: lewo- i prawostronne. Dla definicji Cauchy'ego należy dodać warunek dla y, mianowicie y < x, aby otrzymać funkcję ciągłą lewostronnie. Definicja funkcji ciągłej prawostronnie wymaga zmiany powyższej nierówności na przeciwną. Definicja Heinego wymaga wybrania dowolnego ciągu zbliżającego się do x wyłącznie punktami z lewej lub prawej strony.
Przykłady
Rozpatrujemy funkcje 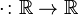 .
.
- Wszystkie
funkcje elementarne
są ciągłe (co jest również prawdą dla funkcji
 ).
). - Funkcja dana wzorem

- jest ciągła.
Przestrzenie metryczne i unormowane
W przestrzeniach
metrycznych
i
przestrzeniach unormowanych
stosuje się nieznacznie tylko zmodyfikowane wersje definicji Cauchy'ego zastępując każdą
wartość bezwzględną
różnicy odpowiednią dla każdej przestrzeni metryką lub normą różnicy.
Dla przestrzeni metrycznych (X,dX) oraz (Y,dY) funkcja  jest ciągła, jeśli prawdziwy jest wzór
jest ciągła, jeśli prawdziwy jest wzór
 .
.
Powyższą implikację można zapisać również w postaci
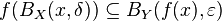
albo
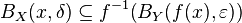 ,
,
gdzie  są
kulami
odpowiednio w
są
kulami
odpowiednio w  , a w nawiasach po oznaczeniu kuli piszy się jej środek i promień.
, a w nawiasach po oznaczeniu kuli piszy się jej środek i promień.
Przestrzenie topologiczne
Ciągłość funkcji w punkcie: dla otoczenia V punktu f(x) możemy znaleźć otoczenie U punktu x takie, że f(U) jest zawarte w V (czyli U jest zawarte w przeciwobrazie V)
Najpełniejszą oraz najogólniejszą definicję ciągłości wprowadza się w topologii.
Niech (X,τX) oraz (Y,τY) będą
przestrzeniami topologicznymi
, a  przekształceniem między nimi. Powiemy, że f jest ciągłe, jeśli
przeciwobraz
dowolnego
zbioru otwartego
w Y jest zbiorem otwartym w X, co zapisuje się następująco:
przekształceniem między nimi. Powiemy, że f jest ciągłe, jeśli
przeciwobraz
dowolnego
zbioru otwartego
w Y jest zbiorem otwartym w X, co zapisuje się następująco:
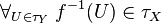 .
.
Równoważnie można wymagać, aby przeciwobraz zbioru domkniętego był domknięty. Jeśli przestrzenie  są
metryzowalne
, to powyższa definicja zgadza się z definicją ciągłości w sensie Cauchy'ego podaną wyżej.
są
metryzowalne
, to powyższa definicja zgadza się z definicją ciągłości w sensie Cauchy'ego podaną wyżej.
Własności
Funkcja rzeczywista, której dziedziną jest przedział domknięty
Jeśli funkcja ![f\colon [a, b] \to \mathbb R](http://upload.wikimedia.org/math/c/d/6/cd6f497f36429e9b3f765e8b4d3176ee.png) jest ciągła, to f na swojej dziedzinie
jest ciągła, to f na swojej dziedzinie
Topologia
Niech (X,τX) i (Y,τY) będą
przestrzeniami topologicznymi
oraz 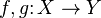 .
.
Aby sprawdzić ciągłość funkcji f, nie trzeba badać wszystkich elementów topologii danej przestrzeni, lecz wystarczy to zrobić dla pewnej jej
bazy
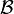 :
:
 .
.
Ciągłość można także badać za pomocą
zbiorów domkniętych
. Mianowicie, funkcja f jest ciągła, jeżeli zachodzi jakikolwiek z następujących warunków:
- przeciwobraz dowolnego zbioru domkniętego w Y jest domknięty w X;
- dla każdego zbioru
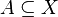 mamy
mamy 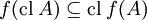 , gdzie
, gdzie  jest operatorem
domknięcia
;
jest operatorem
domknięcia
; - dla każdego zbioru
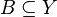 zachodzi
zachodzi  .
.
Przy przekształceniach ciągłych zachowywane są takie własności przestrzeni jak:
Jeśli zbiór D jest
gęsty
w X, f i g są ciągłe, oraz  , to f = g.
, to f = g.
Niech  oraz
oraz  będzie
produktem Tichonowa
, wówczas dla
będzie
produktem Tichonowa
, wówczas dla 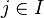 przekształcenie
przekształcenie

jest ciągłym rzutem na j-tą współrzędną.
Przestrzeń funkcji ciągłych
W topologii i analizie funkcjonalnej często bada się przestrzeń, której elementami są funkcje ciągłe z pewnej przestrzeni topologicznej X w inną Y. Taka przestrzeń jest oznaczana symbolem  i jest szczególnym przypadkiem
przestrzeni funkcyjnej
.
i jest szczególnym przypadkiem
przestrzeni funkcyjnej
.
Jednym z najbardziej popularnych przykładów są przestrzenie funkcji ciągłych o wartościach w
liczbach rzeczywistych
.
Pierścień
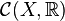 o elementach będących odwzorowaniami ciągłymi z X w
o elementach będących odwzorowaniami ciągłymi z X w  i operacjach algebraicznych wprowadzanych „punktowo” jest ważnym obiektem topologicznym. Przeprowadzono wiele badań w poszukiwaniu związków struktury algebraicznej tego pierścienia ze strukturą topologiczną przestrzeni (X,τX).
i operacjach algebraicznych wprowadzanych „punktowo” jest ważnym obiektem topologicznym. Przeprowadzono wiele badań w poszukiwaniu związków struktury algebraicznej tego pierścienia ze strukturą topologiczną przestrzeni (X,τX).
Na przestrzeni 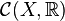 rozważa się także strukturę topologiczną wprowadzając topologie:
rozważa się także strukturę topologiczną wprowadzając topologie:
- zbieżności punktowej,
- zgodną z
topologią Tichonowa
na iloczynie
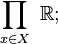
- zbieżności jednostajnej,
- w której
bazą otoczeń
punktu
 jest
jest  , gdzie
, gdzie  .
.
Pojęcie teorio-mnogościowe
Niech  oraz
oraz  będą
porządkami zupełnymi
, wtedy funkcja
będą
porządkami zupełnymi
, wtedy funkcja  jest ciągła, jeżeli zachowuje kresy górne
podzbiorów skierowanych
, tzn:
jest ciągła, jeżeli zachowuje kresy górne
podzbiorów skierowanych
, tzn:
Niech  będzie
podzbiorem skierowanym
, wtedy
będzie
podzbiorem skierowanym
, wtedy 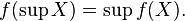
Zobacz też